supergravity
파이썬 - 이진 탐색(binary search) 본문
목차
-시작
-이진 탐색 알고리즘
-이진 탐색 감잡기
-tree 자료구조와 이진 탐색
-시간복잡도
-구현
-bisect 라이브러리
-정리
시작
binary search algorithm에 대해서 알아봅시다.
binary search algorithm은 한국어로 이진 탐색 알고리즘이라고 불리고 있습니다.
이번 글에서 이진 탐색 알고리즘이라고 부르겠습니다.
이진 탐색은 탐색 방법의 한 종류입니다.
이진 탐색은 정렬된 리스트가 있을 때 target과 같은 값이 리스트에 있는지 찾는 탐색 방법입니다.
이진 탐색은 이름을 보면 어떤 알고리즘 인지 대략적으로 이해할 수 있습니다.
이름의 이진은 두 부분으로 라는 뜻을 가지고 있습니다.
그래서 이진 탐색은 "두 부분으로 나누어 찾는 방법이다"라고 이해할 수 있습니다.
이진탐색 알고리즘
이진탐색 감잡기
그러면 구체적으로 이진 탐색 알고리즘이 어떻게 작동하는지 예를 통해 살펴봅시다.
이진 탐색 알고리즘의 인풋으로
sorted_list : [2, 4, 6 ,10, 11, 13, 14]
target_num : 6
이 들어왔다고 생각을 해봅시다.
NOTE: 정렬된 리스트가 아니면 이진 탐색을 진행하지 못합니다.
의문점이 들어도 좀만 버티세요.
조금 있으면 의문점이 풀릴 것입니다.
가장 먼저 sorted_list의 중앙값이 target_num과 같은지 확인합니다.
만약 target_num이 중앙값과 다르면 크기를 비교합니다.
만약 중앙값이 target_num보다 크면, 타깃은 중앙값보다 왼쪽에 위치했다고 확신을 할 수 있습니다.
그 이유는 인풋으로 받은 어레이가 오름차순으로 정렬되어 있기 때문입니다.
만약 중앙값이 타깃보다 작으면 타깃은 오른쪽에 있다고 확신할 수 있습니다.
자 그럼 위의 예시를 이진 탐색 방법으로 탐색해 봅시다.

타깃 6의 경우 중앙값 10보다 작기 때문에 중앙값보다 왼쪽에 존재합니다.
정확한 6의 위치를 찾기 위해 10의 왼쪽에서 아까와 같은 패턴을 반복합시다.
중앙값 4는 6보다 작기 때문에 타깃은 6은 4의 오른편에 존재합니다.
4의 오른편에는 숫자 1개만 존재하고 타깃 6과 같은 숫자입니다.
그래서 4의 오른편에 있는 6의 위치를 리턴합니다.
tree 자료구조와 이진 탐색
이진 탐색 알고리즘을 시각적으로 표현하여 보다 직관적으로 이해해 봅시다.
이를 위해서 인풋으로 받은 정렬된 어레이를 아래의 그림과 같이 표현해 봅시다.
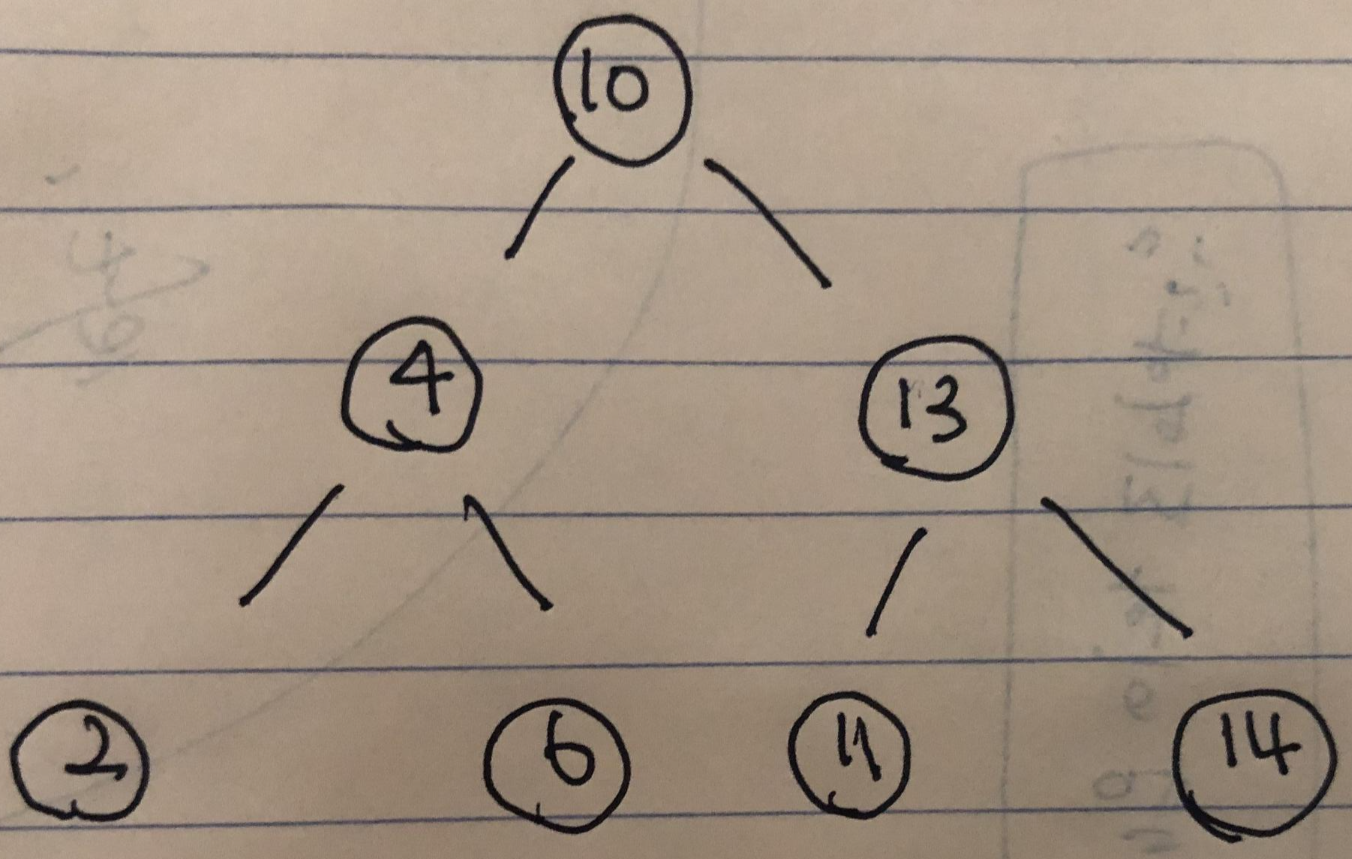
이 표현에서 10은 인풋 어레이의 중앙값을 나타냅니다.
그 아래의 4와 13은 10을 기준으로 반을 쪼개었을 때 중앙값을 나타냅니다.
이런 식으로 정렬된 리스트를 표현하면.
이진 탐색 알고리즘을 보다 직관적으로 나타낼 수 있습니다.
그러면 이전과 동일한 타깃 넘버 6의 위치를 찾아봅시다.

처음으로 맨 위에 있는 10과 타깃 넘버 6을 비교합니다.
6은 10보다 작기 때문에 10의 왼쪽으로 이동합니다.
4와 6을 비교합니다.
6은 4보다 크기 때문에 오른쪽으로 이동합니다.
6과 6을 비교합니다.
같기 때문에 6의 위치를 리턴합니다.
시간복잡도
리스트에서 특정 값을 찾는 기본적인 알고리즘으로 선형 탐색 알고리즘이 있습니다.
선형 탐색의 경우 루프를 돌며 앞에서부터 차례대로 확인을 합니다.
운이 좋게도 타깃 넘버가 어레이의 맨 앞에 존재한다면 단번에 찾을 수 있습니다.
하지만 타깃 넘버와 같은 값이 리스트의 맨 마지막에 존재한다면 루프를 n번 수행하여야 합니다.
이는 O(n)의 시간 복잡도를 가지는 알고리즘이라 말할 수 있습니다.
이진 탐색의 경우 선형 탐색과 달리 인풋으로 들어오는 리스트가 정렬되어 있어야 합니다.
이진 탐색의 시간복잡드는 O(logn)입니다.
그래서 n이 클 때 선형 탐색 시간 복잡도 O(n)에 비해 훨씬 빠릅니다.
이진 탐색의 경우 시간복잡도가 O(logn)입니다.
O(logn)은 정렬된 리스트를 tree로 표현했을 때.
직관적으로 구할 수 있습니다.
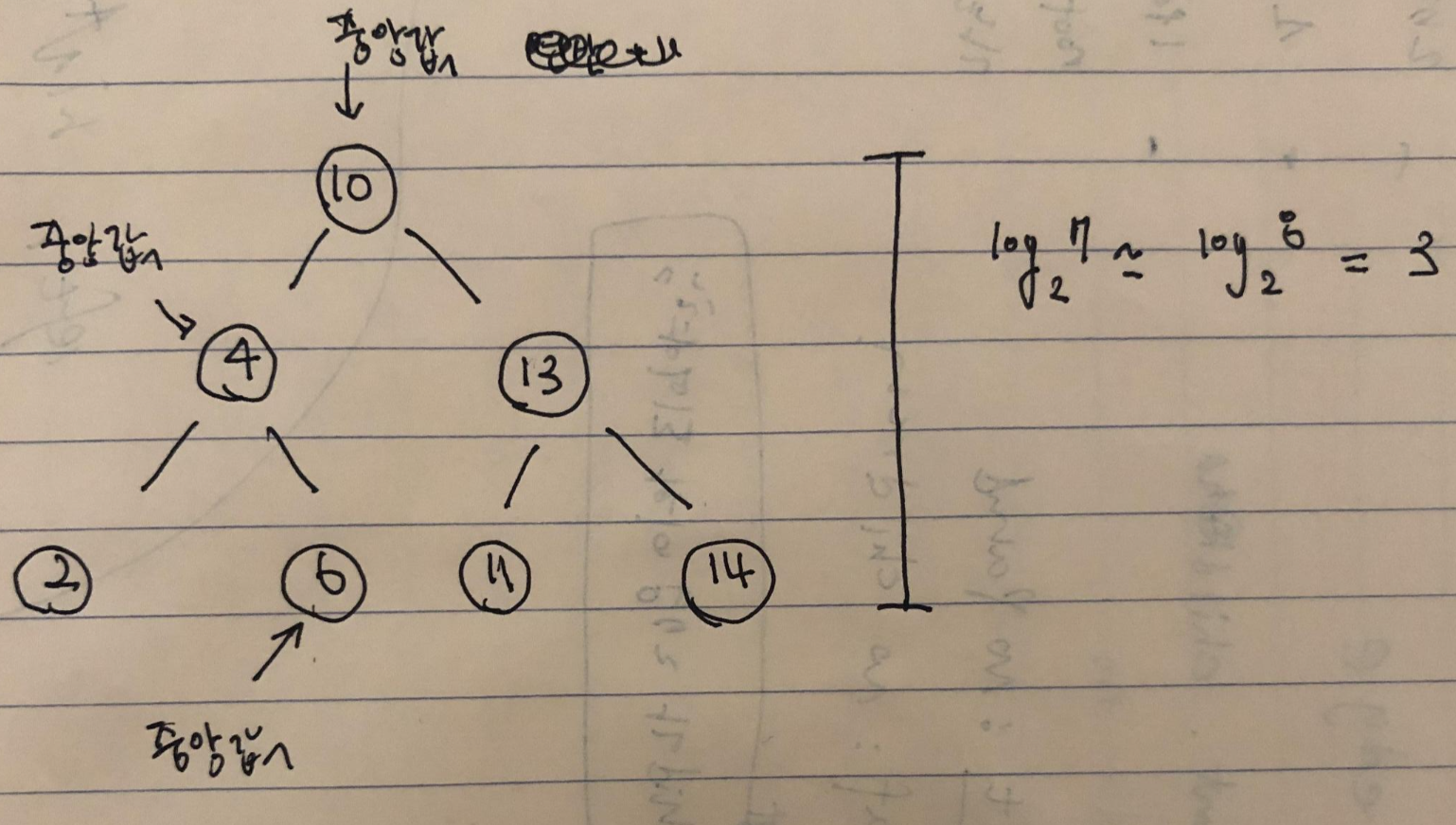
sorted_list를 트리로 표현하고 target_num을 찾기 위해.
3번의 시도를 해야 했었습니다.
위의 그림을 보면 3번의 시도는 tree의 높이에 해당한 다는 것을 볼 수 있습니다.
tree의 높이의 경우 log(node의 수)로 구할 수 있습니다.
결국 이진 탐색 알고리즘은 tree의 높이만큼 수행해야 합니다.
이진 탐색 알고리즘의 시간복잡도는 O(logn)입니다.
구현해보기
인풋으로 target과 sorted_list를 받고.
target이 sorted_list에 삽입되었을 때 정렬이 유지되는 위치를 return 하는
함수를 이진 탐색 방법을 이용하여 구현해 봅시다.
note : 위의 예시와 다른 예시입니다.
위의 예시는 target이 sorted_list에 있는지 확인하는 알고리즘이었습니다.
arr = [2, 4, 6 ,10, 11, 13, 14]
target = 6
def binary_search(arr, target):
s = 0
e = len(arr) - 1
m = (e + s) // 2
while( True ):
if s == m: return s
if arr[m] <= target:
s = m
m = (e + s) //2
elif arr[m] > target:
e = m
m = (e + s) //2
binary_search(arr, target)bisect 라이브러리
bisect 라이브러리에는 bisect_left()와 bisect_right()이 있습니다.
bisect_left의 경우 아래 그림에서 볼 수 있듯.
정렬을 유지할 수 있는 왼쪽 위치를 리턴합니다.
bisect_right의 경우 정렬을 유지할 수 있는 오른쪽 위치를 리턴합니다.

참고로 위에서 구현한 코드는 bisect_right()와 같은 기능을 합니다.
arr = [6,6,7,7,7,8,8,9,10]
target = 7
def binary_search(arr, target):
s = 0
e = len(arr) - 1
m = (e + s) // 2
while( True ):
if s == m: return s
if arr[m] <= target:
s = m
m = (e + s) //2
elif arr[m] > target:
e = m
m = (e + s) //2
binary_search(arr, target)여기서 조금만 변경하면.
bisect_right()과 같은 기능을 하는 함수를 만들 수 있습니다.
각자 해봅시다.
정리
이진 탐색의 가장 중요한 부분은 정렬된 리스트에 대해 적용 가능하다는 점입니다.
이에 대해 명확하게 이해를 넘어서 익히고 있어야 합니다.
이진 탐색의 응용문제는 어떤 기준으로 정렬되어 있는지 알아차려야 해결 가능합니다.
이에 대해 궁금하다면 여기를 클릭합시다.
'콘텐츠 > 파이썬-알고리즘 기초_ 2021' 카테고리의 다른 글
| 파이썬 - 다이나믹 프로그래밍(dynamic programming) 실전 문제 (0) | 2021.11.01 |
|---|---|
| 파이썬 - 최단 경로(shortest path) (0) | 2021.11.01 |
| 파이썬 - graph,DFS, BFS (0) | 2021.10.27 |
| 파이썬 - sorted() (0) | 2021.10.26 |
| 파이썬 - 재귀함수(recursion) (0) | 2021.10.26 |


