supergravity
파이썬 - 이진탐색(binary search) 실전 문제 본문
목차
-시작
-프로그래머스 3단계 : 입국 심사
-프로그래머스 3단계 : 금과 은 운반하기
-프로그래머스 3단계 : 징검다리 건너기 (카카오)
-프로그래머스 4단계 : 징검다리
-정리
시작
이전에 학습한 내용에서 아래와 같은 상황이었습니다.
if target > list[mid]: <<<<<<< 요기를 수정해야 하는 유형들이 나옴
start = mid
mid = (start+mid)//2
else:
end = mid
mid = (start+mid)//2이진 탐색에서는 target과 비교하는 부분에서 변형되어 문제들이 출제됩니다.
target부분을 명확하게 생각하기 위한 프로세스가 있는데,
아래와 같습니다.
1. 임이의 mid에 대해 생각해 보기.
2. 임이의 mid에 대해 어떤 기준을 정했을 때 정렬된 형태가 되는지 << 가장 중요
3. 만약 2번에서 뇌정지가 온다면 그림을 그려 보기
이점을 염두에 두고 진행합시다.
프로그래머스 3단계 : 입국 심사
https://programmers.co.kr/learn/courses/30/lessons/43238
코딩테스트 연습 - 입국심사
n명이 입국심사를 위해 줄을 서서 기다리고 있습니다. 각 입국심사대에 있는 심사관마다 심사하는데 걸리는 시간은 다릅니다. 처음에 모든 심사대는 비어있습니다. 한 심사대에서는 동시에 한
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
입국심사
입국을 대기하는 사람이 1,000,000,000으로 졸라게 많습니다.
이 인원이 심사자에게 심사를 받습니다.
심사자는 100,000로 비교적 작습니다.
심사자는 심사자마다 입국 면접을 보는 시간이 다르고 이를 리스트로 가지고 있습니다.
이때 입국 대기자를 처리하는 최소 시간을 구하는 문제입니다.
문제 읽고 바로 해야 하는 생각
입국 대기자를 보면 졸라게 많습니다.
일단 입국 대기자만 for loop를 처리해도 시간 초과를 받는다는 것을 인지해야 합니다.
그리고 저리 많은 숫자를 보면 이진 탐색 인진 의심을 해봐야 합니다.
문제 분석과 생각의 흐름.
이제 문제를 명확하게 이해하고 어떤 전략을 짤지 생각해 봐야 합니다.
일단 심사자는 100,000명으로 작기 때문에 정렬과 for loop정도는 사용할 수 있습니다.
자유도가 높으니 심사자 입장에서 먼저 생각해 봅시다.
제시된 예제에 대해서 그래프를 그려보았습니다.
네모 6칸을 포함하는 최소 시간이 28인 것을 알 수 있습니다.

이를 통해 임의의 시간이 주어지면,
가장 효율적으로 심사위원이 처리를 했을 때 처리된 입국 대기자 수를 얻을 수 있다는
사실을 명확히 알 수 있습니다.
위의 사실을 정리하기 위해,
시간과 처리 인원에 대한 표를 그려 보았습니다.

처리된 인원이 시간에 따라 정렬된 형태로 등장하는 것을 알 수 있습니다.
여기서 입국 인원이 6일 때 처리된 인원이 6인 것들 중 시간이 가장 짧은 28을 선택해야 합니다.
이걸 무지 성 for loop(순차 탐색)로 처리할까?
생각할 수도 있지만,
시간의 최댓값은 (가장 심사가 느린 사람의 시간) * (입국 대기자 인원)이고
최악의 경우 = (1,000,000,000) *(1,000,000,000)이다.
그러니 이를 이진 탐색으로 처리합시다.
그러면 log(최악의 경우) = 60으로 무진장 빠르게 탐색 가능합니다.
정리와 구라코드
1, times를 정렬한다.
2. 초기 조건을 세팅한다. s = 0, e = times [-1], m = (e + s) //2
3. 이진 탐색을 구현한다.
if s == m: return m
3.1. is_ck_people :시간 m에 대하여 최대 처리 인원을 구한다.
last = bisect_left(times, m)로 m보다 심사시간이 큰 인원을 제외한다.
is_ck_people = 0
for i in range(last):
is_ck_people += m//times [i]
3.2 is_ck_people을 n과 비교하여 시간을 줄일 수 있는지 늘려야 하는지 선택한다.
if is_ck_people >= n: 시간을 줄여!
e = m
m = (e+s) // 2
if is_ck_people < n: 시간을 늘려야 해!
s = m
m = (e+s) //2구현
테스트 케이스에서 28이 아닌 27이 나와.
마지막에 m+1로 수정후 제출
from bisect import bisect_left
def solution(n, times):
answer = 0
times.sort()
s = 0
e = times[-1]*n
m = (e+s) // 2
while(True):
if s == m or e == m or s > e: return m + 1
last = bisect_left(times, m)
is_ck_people = 0
for i in range(last):
is_ck_people += m // times[i]
if is_ck_people >= n:
e = m
m = (e+s) // 2
if is_ck_people < n:
s = m
m = (e+s) //2프로그래머스 3단계 : 금과 은 운반하기
https://programmers.co.kr/learn/courses/30/lessons/86053
코딩테스트 연습 - 금과 은 운반하기
어느 왕국에 하나 이상의 도시들이 있습니다. 왕국의 왕은 새 도시를 짓기로 결정하였습니다. 해당 도시를 짓기 위해서는 도시를 짓는 장소에 금 a kg과 은 b kg이 전달되어야 합니다. 각 도시에는
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
문제는 대략 이렇습니다.
문제가 너무 길기 때문에 위의 링크에서 읽고 다시 봅시다.
문제를 읽고 드는 생각
이 문제를 보면 이진 탐색 문제인 것을 알아차려야 합니다.
일단 시간이 엄청 크고 임의의 시간에 대하여 각 도시들이 최대로 운반할 수 있는 금+은의 양은 정해져 있습니다.
이진 탐색을 눈치채고 문제를 봐봅시다.
임의의 시간 t에 대하여 금+은의 양은 일정합니다.
시간 t에서 운반 가능한 조합은 생각보다 많이 있습니다.
그럼 일단 모든 조합을 생각해 봅시다.
형태
coms = (금, 은)
조건
1. 0 <= 금 <= g_max
2. 0 <= 은 <= s_max
3. 금 + 은 <= 시간 t에서 최대로 운반 가능한 양3번의 조건의 경우 1번 2번 조건에 의해서 부등호가 추가되었습니다.
임의의 시간 t에서 위의 조합 coms = (금, 은)과 인풋 값으로 주어진 (a, b)와 비교하여 시간을 늘릴 것인지 아닌지 판단하면 될듯합니다.
약간 bfs, dfs실전 문제에서 알고리즘은 그대로 사용하고 visited조건을 변형하는 맥락과 비슷합니다.
좀 더 명확하게 하기 위해 그래프를 그려봅시다.
임의의 시간 t에서 총 운반 가능한 경우에 대해 고려합시다.
시간에 따라 총량이 정해지고 기울기가 1인 직선의 형태를 보입니다.
그래프는 g + s = const(총량)와 같은 형태입니다.
g의 최댓값 g_max는 g를 우선적으로 이동했을 때 값입니다.
s의 최댓값 s_max는 s를 우선적으로 이동했을 때 값입니다.
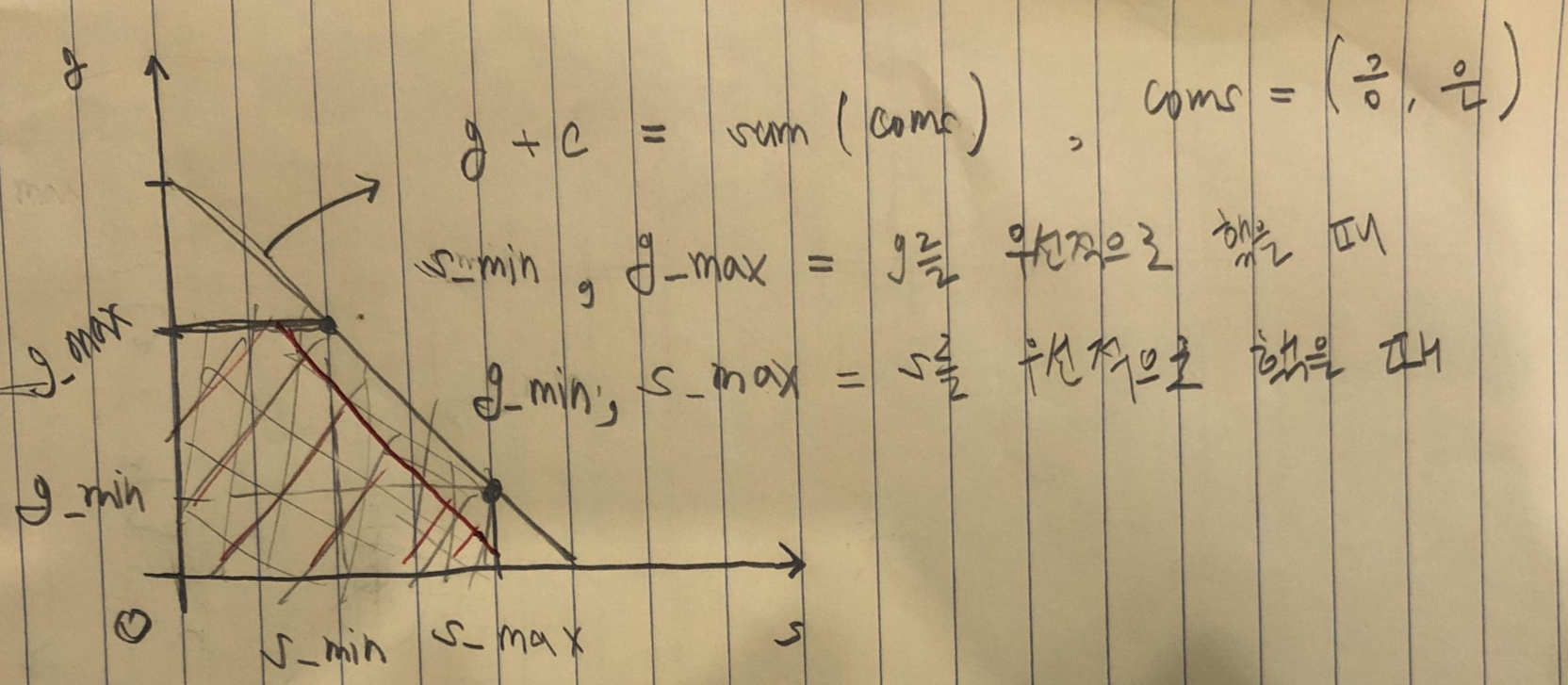
그림의 빨간 직선은 현재 보다 작은 시간에 대한 직선입니다.
빨간 부분의 영역은 현재 영역의 부분집합입니다.
따라서 시간에 따라서 위와 같은 조건을 주었을 때 정렬되어 있습니다.
색칠된 공간에 (a, b)가 존재하면 시간 t에서 (a, b)를 만들 수 있습니다.
그래서 영역에 포함이 되면 시간을 늘리고 영역에 포함되지 않으면 시간을 줄이며 binary search를 진행하면 될듯합니다.
약간 여기서 이해가 안 될 수도 있는데,
list = [ 2, 2, 3, 3, 3 ,3 ,4 ,4, 4]에서
start = 0, end = 8, mid = 4의 상황에서 target 5를 이진 탐색한다고 생각해봅시다.
그럼 아래와 같은 그림이 그려집니다.
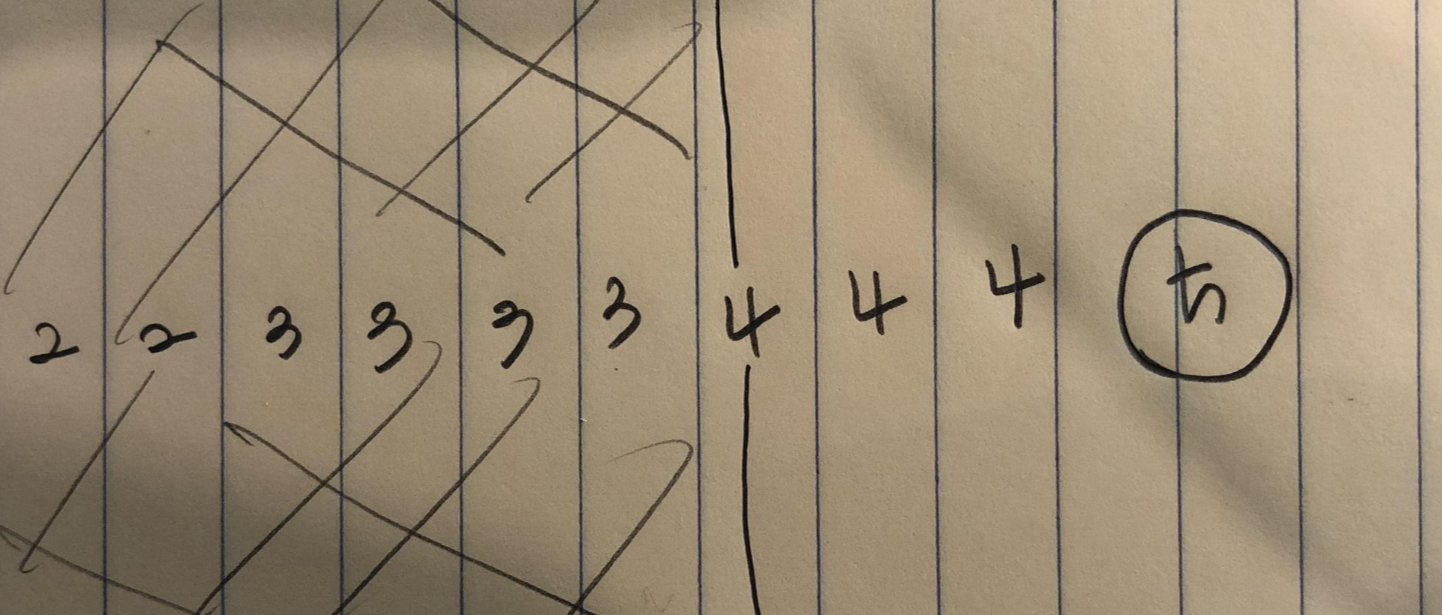
색칠한 영역과 아닌 영역으로 나뉘며,
만약 타깃이 색칠한 영역에 존재하면 end = min로 설정하고,
색칠하지 않은 영역에 존재하면 start = mid로 설정하며 이진탐색을 진행합니다.
같은 맥락으로 가능한 영역을 둘로 나누고 이진탐색을 진행하면 됩니다.
의사 코드
1. 이진 탐색 구현
2. 금을 우선적으로
3. 은을 우선적으로
4. 금_우선 >= a, 은_우선 >= b, 총량 >= a+b
시간을 줄여야함
아닌 경우
시간을 늘려야함구현
def solution(a, b, g, s, w, t):
start = 0
end = 9999999999999999
mid = (start + end ) // 2
while True:
if start == mid:
break
g_max, g_min, s_max, s_min = 0, 0, 0, 0
for i in range(len(t)):
factor = (mid+t[i])//(2*t[i])
g_max += g[i] if factor*w[i] - g[i] > 0 else factor*w[i]
s_min += min(s[i], factor*w[i] - g[i]) if factor*w[i] - g[i] > 0 else 0
s_max += s[i] if factor*w[i] - s[i] > 0 else factor*w[i]
g_min += min(g[i], factor*w[i] - s[i]) if factor*w[i] - s[i] > 0 else 0
if g_max >= a and s_max >= b and g_max+s_min >= a + b:
end = mid
mid = (start + end)//2
else:
start = mid
mid = (start + end)//2
return mid + 1프로그래머스 3단계 : 징검다리 건너기 (카카오)
https://programmers.co.kr/learn/courses/30/lessons/64062
코딩테스트 연습 - 징검다리 건너기
[2, 4, 5, 3, 2, 1, 4, 2, 5, 1] 3 3
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
문제는 대략 이렇습니다.
문제가 너무 길기 때문에 위의 링크에서 읽고 다시 봅시다.
문제를 읽고 드는 생각
부분 점수가 있습니다.
무지성 완전탐색으로 해결하면 0.5점 정도는 가능합니다.
예제에 나온 상황과 동일하게 구현하면 될듯합니다. 의사 코드 정도만 생각해 봅시다.
1. '사람 수'에 대해서 for loop를 돈다.
2. stones의 모든 성분에 -1을 한다.
3. -1를 할때 연속된 0의 수를 카운트한다.
4. 연속된 0이 k보다 크거나 같으면 '사람수'를 리턴한다.위와 같이 구현하게 되면,
상황에 따라 '사람 수'가 2억까지 올라갈 수 있어 O(2억)의 시간복잡도가 소요됩니다.
자 여기서 '사람 수'가 무진장 큽니다.
그러니 이진 탐색을 의심해 봅시다.
'사람 수'에 따라 모두 이동이 가능한지를 표로 생각해 봅시다.
| 사람 수 | 0 | 1 | 2 | ..... | max_num | max_num+1 | ||
| 가능? | 1 | 1 | 1 | ..... | 1 | 0 | 0 | 0 |
요런식으로 구성됩니다.
여기서 1은 모두 이동 가능한 경우이고 0은 모두 이동 불가능한 경우입니다.
위의 표는 정렬되어있습니다.
그러니 이진탐색 알고리즘을 사용할 수 있습니다.
의사코드
1. 이진탐색을 진행한다. target은 사람수이다.
def is_ok() --> bool
2. mid가 가능한지 조사한다.
3. stones의 loop를 돌며 연속된 0의 부분 수열의 길이를 조사한다.
4. 만약 연속된 부분 수열의 최대값이 k보다 크거나 같으면 불가능 하다.
5.is_ok()가 거짓이면 사람의 수를 줄여야한다.
end = mid로 계산한다.
6.참이면
start = end로 계산한다.구현
def solution(stones, k):
start = 0
end = max(stones)
mid = (start + end)//2
while True:
if start == mid: return mid + 1
if is_ok(stones, k, mid):
start = mid
mid = (start + end)//2
else:
end = mid
mid = (start + end)//2
def is_ok(stones, k, mid):
result = []
answer = 0
dum = 0
for stone in stones:
if stone - mid <= 0:
result.append(0)
dum += 1
if dum > answer: answer = dum
else:
result.append(stone - mid)
dum = 0
if answer >= k: return False
return True프로그래머스 4단계 : 징검다리
https://programmers.co.kr/learn/courses/30/lessons/43236
코딩테스트 연습 - 징검다리
출발지점부터 distance만큼 떨어진 곳에 도착지점이 있습니다. 그리고 그사이에는 바위들이 놓여있습니다. 바위 중 몇 개를 제거하려고 합니다. 예를 들어, 도착지점이 25만큼 떨어져 있고, 바위가
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
문제는 대략 이렇습니다.
0부터 시작해 distance길이의 길이 있습니다.
이 길에는 바위들이 놓여있습니다.
놓은 바위는 리스트 형태로 주어집니다.
바위를 n개 제거한 뒤 각 지점 사이의 거리의 최솟값 중에 가장 큰 값을 return 하는 문제입니다.
부분 점수는 먹고 가자
이런 문제는 대부분 부분 점수가 있습니다.
그러니 무지성 완전탐색으로 먼저 풀어봅시다.
combinations를 이용하여 모든 경우의 수를 만들고,
최솟값을 찾아 저장하였다가,
마지막에 최댓값을 리턴하면 됩니다.
from itertools import combinations
def solution(distance, rocks, n):
rocks.sort()
answer = []
for ele in combinations(rocks, len(rocks)-n):
dum = [ele[0]]
for i in range(1, len(ele)):
dum.append(ele[i]-ele[i-1])
dum.append(distance-ele[-1])
answer.append(min(dum))
return max(answer)이 풀이는 시간초과 판정을 받습니다.
왜 그런지 시간복잡도를 계산해 봅시다.
for ele in combinations(rocks, len(rocks)-n)
==> O(50000 * (50000 -1 ) ....*(50000 -len(rocks)-n )
for i in range(1, len(ele)):
===> O(len(rocks)-n)
answer.append(min(dum))
===> O(len(rocks)-n)
결국? O(1조?)combinations에서 진짜 많이 소모합니다.
문제를 읽고 드는 생각
인풋을 보니 k와 distance가 2억입니다.
이분탐색으로 해결하면 좋을 것 같은 문제입니다.
또한 거리의 최솟값 중 최댓값을 구하는 문제이니,
바위 사이의 거리를 이분 탐색 파라매터로 사용하면 될듯합니다.
이 상황은 아래의 그림과 같이 나타낼 수 있으며,
target(바위 사이의 거리)에 대해 정렬되어 있습니다.
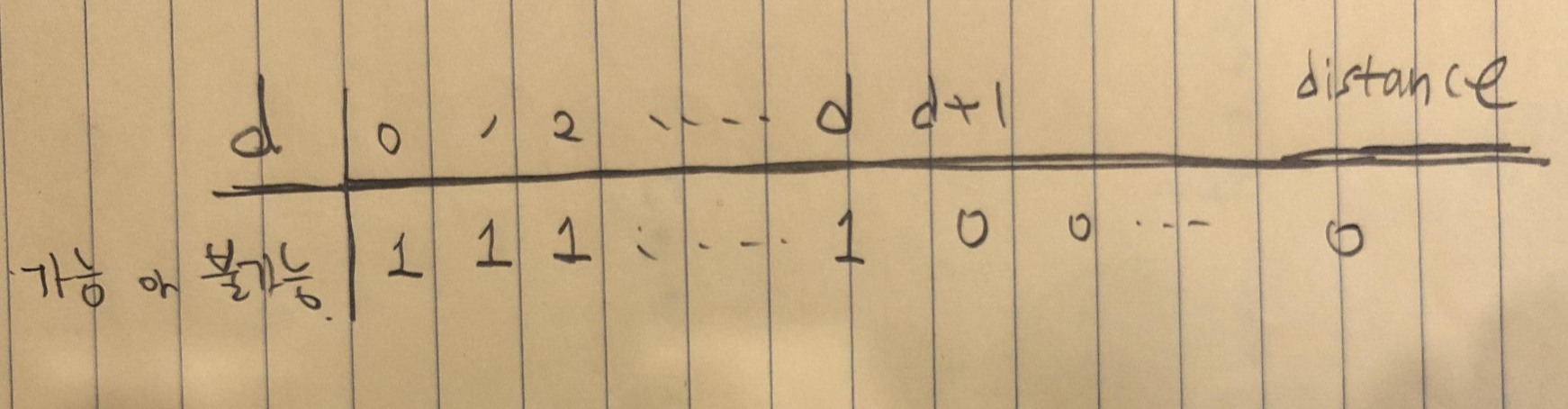
바위 사이의 거리의 최솟값 중 최댓값을 d라 가정해 봅시다.
그럼 rocks에서 n개의 바위를 제거했을 때 가능하지부터 확인해야 합니다.
여기서 약간 센스가 필요한데....
완전탐색을 이용하면 n개를 제거하여 만들 수 있는 집합에 d가 존재하는지 확인하면,
위에서 구현한 무지성 탐색과 같은 방식이라 시간 초과를 받습니다.
완전탐색이 아닌 탐욕적인(그리디) 방법으로 접근해야 합니다.
앞에서부터 거리 차이를 계산하고 만약 d와 비교했을 때 작으면 삭제하는 방식으로,
rocks에서 n개의 바위를 제거하고,
제거된 rocks의 최솟값이 d보다 작거나 같은지 확인해야 합니다.
만약 rocks의 최솟값이 d보다 크면 d를 만족하는 케이스가 없기 때문에,
d를 줄여야 합니다.
의사코드
1. rocks 정렬하기
2. 이분탐색 진행
target = 돌사이의 최대 길이
rocks에서 그리디 방식으로 돌제거
만약 Min(제거된 돌들) < target
불가능.. target 줄여야함
end = mid
else:
start = mid구현
def solution(distance, rocks, n):
rocks.sort()
start = 0
end = distance
mid = (start+end) // 2
while True:
if start == mid: return mid
removed_rocks = remove_rocks(rocks, n, mid )
if is_ok(removed_rocks, mid, distance):
end = mid
mid =(start+end) // 2
else:
start = mid
mid =(start+end) // 2
def remove_rocks(rs, n, t):
stack = [0]
for rock in rs:
stack.append(rock)
while len(stack) >= 2:
if stack[-1]-stack[-2] < t and n != 0:
stack.pop()
n -= 1
else:
break
return stack
def is_ok(removed_rocks, t, distance):
dum = [removed_rocks[0]]
for i in range(1,len(removed_rocks)):
dum.append(removed_rocks[i]-removed_rocks[i-1])
dum.append(distance-removed_rocks[-1])
if min(dum[1:]) < t: return True
return False정리
이진 탐색은 target을 어떻게 처리하냐가 중요합니다.
이에 대해 명확하지 않다면,
구현할 필요가 없습니다.
구현해도 95퍼센트 정도 틀립니다.
만약 명확하지 않다면 아래의 방법을 이용해 봅시다.
1. 임이의 mid에 대해 생각해 보기.
2. 임이의 mid에 대해 어떤 기준을 정했을 때 정렬된 형태가 되는지 << 가장 중요
3. 만약 2번에서 뇌정지가 온다면 그림을 그려 보기
'콘텐츠 > 파이썬-알고리즘 기초_ 2021' 카테고리의 다른 글
| 파이썬 - 다이나믹 프로그래밍(dynamic-programming) 문제 풀이 전략 (0) | 2021.12.13 |
|---|---|
| 파이썬 - merge intervals (0) | 2021.12.04 |
| 파이썬 - graph 실전 문제 (0) | 2021.11.03 |
| 파이썬 - 투 포인터(two pointers) (0) | 2021.11.02 |
| 파이썬 - 다이나믹 프로그래밍(dynamic programming) 실전 문제 (0) | 2021.11.01 |



