supergravity
파이썬 - graph,DFS, BFS 본문
목차
-graph? 어떻게 학습해야 하나
-directed graph, undirected graph
-neighbor
-graph 구현
-graph에 사용되는 기본적인 알고리즘 2개(bfs, dfs)
-문제
graph? 어떻게 학습해야 하나
그래프가 뭘까요?
그래프는 아래의 그림과 같이 원안에 데이터를 포함하는 노드와.
노드들을 연결하는 엣지로 구성됩니다.
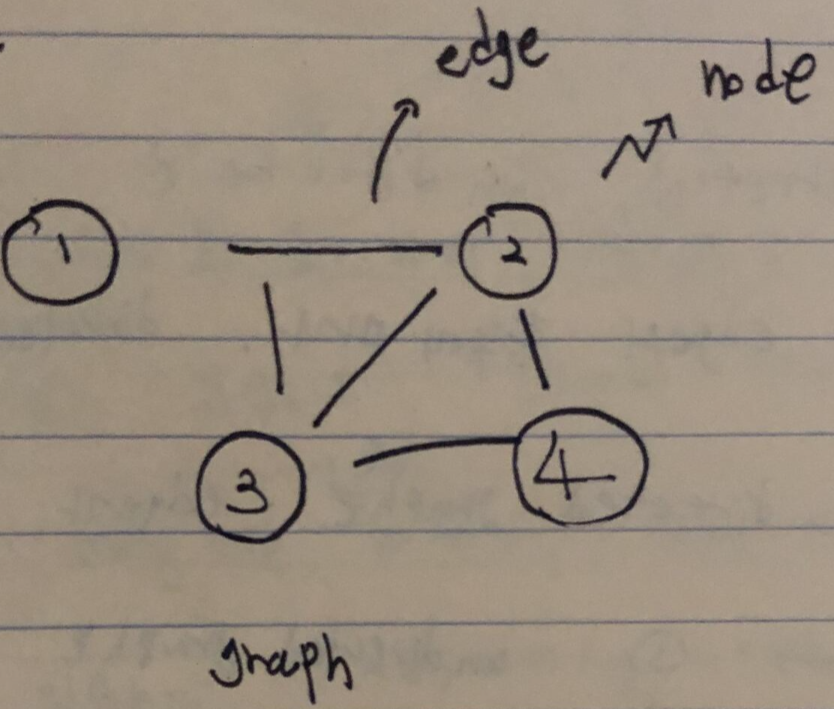
노드와 엣지로 구성된 그래프는 현실 문제를 표현하고 해결하기 참 좋습니다.
그래서 코딩테스트에서는 현실 상활을 응용한 문제들이 출제되고 있습니다.
현실 문제를 그래프로 표현하는 방법은
node를 현실에 존재하는 객체로 표현하고,
엣지를 객체들의 관계로 표현하면 됩니다.
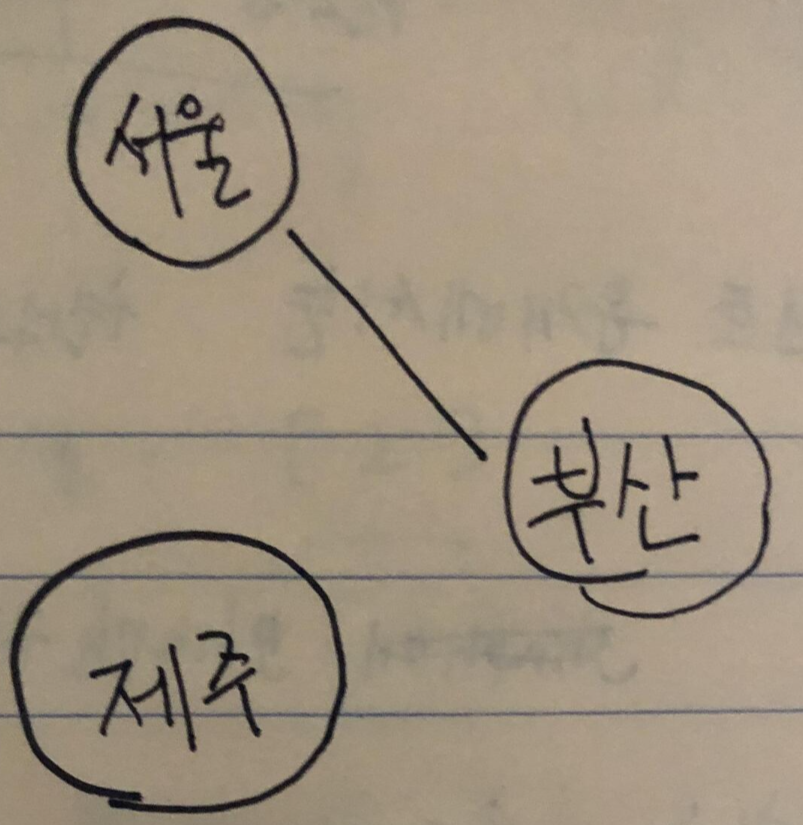
예를 들어 도시의 교통문제를 해결하기 위해
도시와 이들의 관계를 graph로 표현해 보면.
도시는 node로, 도시를 연결하는 도로는 edge로 표현할 수 있습니다.
대부분의 코딩 테스트 문제에서는 현실의 문제를 그래프로 표현한 상활까지 주어집니다.
이 상황에서 그래프의 구조에 사용될 수 있는 적절한 알고리즘을 이용해 답을 제출하면.
정답 판정을 받을 수 있습니다.
그래서 그래프에 사용되는 알고리즘의 특징과 장단점을 알고.
이를 구현할 수 있도록 수련해야 합니다.
directed graph, undirected graph
그래프는 엣지의 종류에 따라 다이렉티드 그래프와 언다이렉티드 그래프로 분류됩니다.
다이렉티드 그래프는 엣지가 방향이 있는 그래프로 엣지는 당방 향을 의미합니다.

언다이렉티드 그래프는 엣지가 방향이 없는 그래프로 엣지는 양방향을 의미합니다.

다이렉티드 그래프 예시의 경우 3번 노드에서 2번 노드로 가기 위해서는.
3 -> 4 -> 2의 경로로 이동을 해야 합니다.
그 반면 언다이렉티드 그래프 예시는 3 -> 2로 바로 갈 수 있을 뿐만 아니라
3 -> 4 ->2의 경로로도 이동 가능합니다.
neighbor
neighbor는 단어에도 알 수 있듯.
주변 노드를 말합니다.
명확한 정의는 이렇습니다.
특정 노드 A에서 바로 다음으로 갈 수 있는 임의의 노드 B는 A의 neighbor라고 정의합니다.
정의를 말하니 뭔가 어렵고 복잡한데.
쉽습니다. 예를 들어 직관적으로 이해합시다.

이전에 사용한 그림을 이용합시다.
이 그래프에서 노드 3의 네이버는 4번 노드입니다.
2번 노드는 4번을 거처 가야 하기 때문에 네이버가 아닙니다.

이 그래프의 3번 노드의 네이버는 2와 4입니다.
3번 노드에서 2번 4번 노드를 바로 접근 가능합니다.
graph 코딩으로 구현
통상적으로 그래프는 adjacency list로 표현하여 사용합니다.
adjacency는 '인접'이라는 뜻을 가지고 있습니다.
그래서 아래에 표현된 adjacency list를 보면.
dictionary 자료구조로 구현되어 있으며.
key에는 모든 노드가 value에는 key node의 모든 네이버를 리스트에 저장되어 있습니다.

근데 adjacency list가 그래프를 완벽히 표현한 것은 맞을까요?
이를 확인해 보기 위해 adjacency list를 분석해 봅시다.
adj list를 한 줄씩 읽으며 그래프를 그려봅시다. 첫 줄을 읽으면 1번 노드가 그려지고. 1번 노드의 네이버로 단방향(화살표가 있는) 2번 5번이 그려집니다. 두 번째 줄을 읽어 봅시다. 2번은 이미 그려져 있으니 네이버를 봅니다. 2번에서 1번으로 가는 단방향을 그립니다. 첫 줄을 읽을 때 1번에서 2번으로 가는 단 뱡향 엣지와 합처. 1번에서 2번을 연결하는 양방향 엣지로 변경합니다........노가다.......이런식으로 모든 adj list를 탐색하며 그래프를 그리면. 위의 예시 그래프와 같은 그래프를 얻는 것을 확인할 수 있습니다.
통상적으로 adj list를 이용하여 그래프를 표현하지만. 모든 노드에 대하여 네이버를 얻을 수 있다면. 어떠한 형태의 구현이라도 그래프를 완벽하게 표현 가능합니다. 그래서 상황에 따라 유연하게 구현하면 좋습니다. 이에 대한 내용은 문제를 풀며 다뤄봅시다.
graph에 사용되는 기본적인 알고리즘 (DFS, BFS)
DFS와 BFS는 그래프의 모든 시작 노드로부터 연결된 모든 노드를 탐색하는 알고리즘입니다.
하지만 탐색 순서에 차이가 있습니다.
DFS는 depth first search의 약자로 깊이를 우선적으로 탐색하는 알고리즘입니다.
BFS의 경우 breadth first search의 약자로 너비를 우선적으로 탐색하는 알고리즘입니다.
처음 보는 입장에서 이런 식으로 말하면.
"그래프의 깊이가 뭐고 너비가 뭔데 우선적으로 탐색한다는 거야 ㅆㅃ"
이라고 생각할 수 있습니다.
그러니 우선적으로 예를 통해 직감적으로 접근합시다.

dfs는 안으로 파고들며 모든 곳을 탐색하는 방법입니다.
dfs에서 1번 다음 두 번째로 5번을 탐색하는데.
2번을 우선적으로 탐색해도 무방합니다.
어차피 모든 곳을 탐색해야 하니 별 문제가 되지 않습니다.
하지만 2번을 선택하더라도 깊이 우선으로 탐색해야 합니다.
2번을 먼저 탐색했다고 생각을 해보면.
1 -> 2 -> 3 -> 4 -> 5 ->6
순으로 탐색을 하게 됩니다.
bfs의 경우에는 주변을 확대해 가며 탐색하는 방법입니다.
bfs는 가까운 곳을 먼저 탐색하기에.
탐색 순서는 시작 노드로부터의 최단거리를 의미합니다.
그래서 최단거리를 구할 때 응용될 수 있습니다.
DFS
DFS를 어떻게 하면 코드로 구현할 수 있을까요?
재귀 함수에 대해 알고 있다면.
재귀로 탐색하는 것과 유사하다고 느낄 겁니다.
실제 재귀함수와 같은 방식으로 작동합니다.
그래서 재귀함수로 DFS를 구현할 수 있습니다.
이에 대해 명확하지 않다면 클릭!
그럼 재귀로 구현해 봅시다.
graph는 adj list로 구현되었습니다. explored를 통해 방문했는지 체크합니다. 만약에 방문 유무를 체크하지 않고 구현하게 되면. 무한 루프에 빠지게 됩니다.
graph = {
1 : [5,2],
2 : [3],
3: [4],
4: [2],
5: [6],
6: [],
}
explored = set()
def dfs(explored, node, graph):
print(node)
explored.add(node)
for n in graph[node]:
if n not in explored:
dfs(explored, n, graph)
dfs(explored, 1, graph)
---> 출력결과
1
5
6
2
3
4
근데 recursion call은 stack에 저장했다가 사용하는 걸로 알고 있는데.
stack으로도 구현이 가능하지 않을까?
그렇습니다. stack으로 구현이 가능합니다.
stack 자료구조에 대해 명확하지 않다면 클릭!
그럼 스택으로 구현해 봅시다.
graph = {
1 : [5,2],
2 : [3],
3: [4],
4: [2],
5: [6],
6: [],
}
explored = set()
stack = [1]
while stack:
current_node = stack.pop()
print(current_node)
explored.add(current_node)
for n in graph[current_node]:
if n not in explored:
stack.append(n)
---->출력결과
1
2
3
4
5
6리커션과 달리 2번 노드가 먼저 탐색이 되지만.
깊이 우선으로 탐색하는 것을 볼 수 있습니다.
BFS
BFS는 어떻게 구현할까요?

동작 과정을 보며 한 번 더 생각해 봅시다.
1. 거리가 0인 곳부터 시작해 +1씩 증가해 가면 탐색하는 것을 볼 수 있습니다.
이를 loop를 통해 구현하면 될 것임을 직감적으로 알 수 있습니다.
2. DFS에서와 마찬가지로 방문처리가 필요합니다.
그렇지 않으면 무한루프에 빠질 것입니다.
2. 거리가 i번째와 i-1번째의 패턴을 보면.
i번쨰 노드들은 i-1번째의 노드의 네이버인 것을 발견할 수 있습니다.
하지만 방문한 적이 있는 노드는 제외해야 무한루프를 면할 수 있을 듯합니다.
이 관찰 결과들을 이용하여 BFS를 구현해 봅시다.
graph = {
1 : [5,2],
2 : [3],
3: [4],
4: [2],
5: [6],
6: [],
}
explored = {}
daum_node = [1]
dist = 0
while daum_node:
dummy = []
for node in daum_node:
print(node)
explored.setdefault(node, dist)
for next_node in graph[node]:
if next_node not in explored:
dummy.append(next_node)
dist += 1
daum_node = dummy
print(explored)
---->출력결과
1
5
2
6
3
4
{1: 0, 5: 1, 2: 1, 6: 2, 3: 2, 4: 3}출력 결과를 보면 너비 우선으로 탐색한 것을 볼 수 있습니다.
또한 dist를 while loop가 끝날 때마다 +1을 해주고 방문 처리할 때 같이 저장했습니다.
그래서 시작 노드에서 임기의 노드로 가는 최단거리도 구할 수 있는 것을 볼 수 있습니다.
while 밑에 dummy는 다음 노드를 저장하기 위해 사용되었습니다.
dummy를 사용하지 않는다면 daum_noe를 순회할 때 daum_node가 변경되어 오류가 생성됩니다.
DFS에서 stack을 이용하여 깔끔하게 구현한 것처럼.
BFS에서는 queue를 이용하면 깔끔하게 구현할 수 있습니다.
queue에 대해서 명확하지 않다면 클릭!
그럼 구현해 봅시다.
DFS의 stack구현을 deque로 변환시키면 끝입니다.
하지만 왜 이러한 현상이 일어나는지는 꼭! 생각을 해봅시다.
응용문제를 풀떄 도움이 됩니다.
stack을 deque로만 변환시키면.
최단거리에 대한 정보가 없습니다.
코드를 수정하여 위의 구현처럼 최단거리를 저장하는 코드도 작성해 봅시다.
from collections import deque
graph = {
1 : [5,2],
2 : [3],
3: [4],
4: [2],
5: [6],
6: [],
}
explored = set()
q = deque([1])
while q:
current_node = q.popleft()
print(current_node)
explored.add(current_node)
for n in graph[current_node]:
if n not in explored:
q.append(n)
---->출력결과
1
5
2
6
3
4
문제
1. 문제: 섬의 수
N*N크기인 2차원 배열이 MAP이 주어집니다.
MAP은 0과 1로 구성되어 있습니다.
0은 바다를 의미하고 1은 육지를 의미합니다.
MAP에 섬의 수가 몇 개인지 리턴하는 함수를 구현하시오.
(N은 1 이상 10 이하입니다.)
문제 분석과 아이디어 도출
N이 작아 무지성으로 전부 탐색하면 될 듯합니다.
MAP의 모든 노드를 방문하며.
1이 나오면 bfs를 실행하고.
리스트의 mutable성질을 이용해.
bfs 또는 dfs를 이용해 인접한 1을 찾고 방문처리를 MAP [i][j] = 0으로 하면.
깔끔하게 해결될 듯합니다.
구라코드
count = 0
for x y 모든 map을 순회
if map[x][y] == 1이면:
bfs()
count += 1구현
1. 그래프 구현( 모든 노드에 대해 네이버를 알 수 있으면 구현이 끝남.)
adj 함수는 인풋으로 받은 노드의
아래, 오른쪽, 왼쪽, 위에 성분이 1인 노드가 있는지 확인하고.
만약 성분이 1이고 MAP의 범위에 벗어나지 않으면.
result에 담았다가.
모든 네이버를 리턴하는 함수입니다.
2. dfs구현
방문처리를 1이었던 노드의 성분을 0으로 변환하는 방법으로 구현하고.
재귀함수를 이용하여 구현했습니다.
MAP = [
[0,1,0,0,1],
[0,1,1,0,0],
[0,0,1,0,0],
[0,0,0,0,0],
[0,1,1,1,0]
]
def adj(map_, node):
result = []
x, y = node
moves = [(1,0), (0,1), (-1,0), (0, -1)]
for move in moves:
nx = x + move[0]
ny = y + move[1]
if 0 <= nx < len(map_) and 0 <= ny < len(map_) and map_[nx][ny] == 1:
result.append((nx, ny))
return result
def dfs(node, map_, adj):
map_[node[0]][node[1]] = 0
ns = adj(map_, node)
for n in ns:
dfs(n, map_, adj)
count = 0
for i in range(len(MAP)):
for j in range(len(MAP)):
if MAP[i][j] == 1:
count += 1
dfs((i,j), MAP, adj)
print("1발견", i, j)
for ele in MAP:
print(ele)
print(count)
---> 출력결과
1발견 0 1
[0, 0, 0, 0, 1]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 1, 1, 1, 0]
1발견 0 4
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 1, 1, 1, 0]
1발견 4 1
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
32. 문제 : 최단 거리
N*N크기인 2차원 배열의 MAP이 주어집니다.
MAP은 0과 1로 구성이 되어있습니다.
0은 길을 의미하고 1은 벽을 의미합니다.
(0,0)에서 (N-1, N-1)로 가는 최단 경로중 1개를 출력하세요.
(N은 1 이상 10 이하입니다.)
문제 분석과 아이디어 도출
인풋이 작아 무지성으로 모든 노드를 bfs로 탐색하면 될듯합니다.
구라코드
bfs와 adj를 구현하면 끝!
구현
MAP = [
[0,1,0,0,1],
[0,1,1,0,0],
[0,0,1,0,0],
[0,0,0,0,0],
[0,1,1,1,0]
]
def adj(map_, node):
result = []
x, y = node
moves = [(1,0), (0,1), (-1,0), (0, -1)]
for move in moves:
nx = x + move[0]
ny = y + move[1]
if 0 <= nx < len(map_) and 0 <= ny < len(map_) and map_[nx][ny] == 0:
result.append((nx, ny))
return result
def bfs(map_):
ns = [(0,0)]
visited ={}
count = 0
while(ns):
dummy = []
for n in ns:
visited.setdefault(n, count)
for a in adj(map_, n):
if a not in visited:
dummy.append(a)
count += 1
ns = dummy
return visited
print(bfs(MAP)[(4,4)])
---> 출력결과
8
3. 문제 : 가장 큰 섬
N*N크기인 2차원 배열이 MAP이 주어집니다.
MAP은 0과 1로 구성되어 있습니다.
0은 바다를 의미하고 1은 육지를 의미합니다.
1로 구성된 섬 중 가장 큰 섬을 리턴하는 함수를 구현하시오
(N은 1 이상 10 이하입니다.)
문제 분석과 아이디어 도출
1번의 방법을 그래로 사용하고.
섬의 크기를 저장하는 코드만 추가하고
그렇게 저장된 섬의 크기 중 가장 큰 값을 리턴하면 될듯합니다.
구라코드
1번에 추가만 합시다.
구현
MAP = [
[0,1,0,0,1],
[0,1,1,0,0],
[0,0,1,0,0],
[0,0,0,0,0],
[0,1,1,1,0]
]
def adj(map_, node):
result = []
x, y = node
moves = [(1,0), (0,1), (-1,0), (0, -1)]
for move in moves:
nx = x + move[0]
ny = y + move[1]
if 0 <= nx < len(map_) and 0 <= ny < len(map_) and map_[nx][ny] == 1:
result.append((nx, ny))
return result
def dfs(node, map_, adj, size):
map_[node[0]][node[1]] = 0
size[0] += 1
ns = adj(map_, node)
for n in ns:
dfs(n, map_, adj, size)
lands = []
for i in range(len(MAP)):
for j in range(len(MAP)):
if MAP[i][j] == 1:
size = [0]
dfs((i,j), MAP, adj, size)
lands.append(size[0])
print(max(lands))
---> 출력결과
4
4. 문제 : 단어 변환
https://programmers.co.kr/learn/courses/30/lessons/43163
코딩테스트 연습 - 단어 변환
두 개의 단어 begin, target과 단어의 집합 words가 있습니다. 아래와 같은 규칙을 이용하여 begin에서 target으로 변환하는 가장 짧은 변환 과정을 찾으려고 합니다. 1. 한 번에 한 개의 알파벳만 바꿀 수
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
코딩테스트 연습
기초부터 차근차근, 직접 코드를 작성해 보세요.
programmers.co.kr
문제 설명
인풋으로 begin target words가 주어집니다.
begin의 단어를 target으로 변화시켜야합니다.
변화는 아래의 규칙을 따르며 가장 짧은 변환 과정을 찾으려고 합니다.
1. 한 번에 한 개의 알파벳만 바꿀 수 있습니다.
2. words에 있는 단어로만 변환할 수 있습니다.
문제 분석과 아이디어 도출
문제를 분석하기 위해 주어진 예제에 대해 그림을 그려봅시다.
begin : "hit, target : "cog", words: ["hot", "dot", "dog", "lot", "log", "cog"]
문제 조건을 따라 그림을 그려보면.
아래와 같은 그래프가 생성됩니다.

구라코드
def adj():
words를 루프돌며, 같은 문자가 2개인지 확인
같은 문자가 2개인 문자들 리턴
def BFS():
bfs노가다....구현
begin = "hit"
target = "cog"
words = ["hot", "dot", "dog", "lot", "log", "cog"]
def adj(node, words):
result = []
for word in words:
count = 0
for w, n in zip(word, node):
if w == n:
count += 1
if count == 2:
result.append(word)
return result
def bfs(begin, adj, words):
ns = [begin]
explored = {}
count = 0
while ns:
dummy = []
for n in ns:
explored.setdefault(n, count)
for a in adj(n, words):
if a not in explored:
dummy.append(a)
count += 1
ns = dummy
return explored
a = bfs(begin, adj, words)
print(a['cog'])
print(a)
---> 출력결과
4
{'hit': 0, 'hot': 1, 'dot': 2, 'lot': 2, 'dog': 3, 'log': 3, 'cog': 4}
'콘텐츠 > 파이썬-알고리즘 기초_ 2021' 카테고리의 다른 글
| 파이썬 - 최단 경로(shortest path) (0) | 2021.11.01 |
|---|---|
| 파이썬 - 이진 탐색(binary search) (0) | 2021.10.28 |
| 파이썬 - sorted() (0) | 2021.10.26 |
| 파이썬 - 재귀함수(recursion) (0) | 2021.10.26 |
| 파이썬 - 순열, 조합 (permutaions, combinations) (0) | 2021.10.25 |


