supergravity
파이썬 - 다이나믹 프로그래밍 실전 문제(new version) -- 준비중 본문
목차
시작
매트릭스에서 DP
- 문제 1 : 최소비용으로 목적지까지 도달하기
- 문제 2: 공 낙하 실험
- 문제 3: [카카오 인턴] 경주로 건설
연속된 부분 처리하는 유형
- 문제 1: 증가하는 가장 큰 수열 만들기
- 문제 2: 최장 공통부분 수열
- 문제 3: 두 리스트의 가장 긴 공통부분 찾기
- 문제 4: 복수전공 수강 신청
- 문제 5: [카카오 인턴] 보석 쇼핑
- 문제 6: [카카오 블라인드] 광고 삽입
이전의 영역에서 선택되어 오는 경우
- 문제 1: Min Cost Climbing Stairs
- 문제 2: Coin Change
- 문제 3: Word Break
- 문제 4: Best Time to Buy and Sell Stock IV
- 문제 5: Best Time to Buy and Sell Stock with Transaction Fee
- 문제 6: Best Time to Buy and Sell Stock with Cooldown
- 문제 7: Minimum Cost For Tickets
경우의 수를 찾는 유형
- 문제 1: Coin Change 2
- 문제 2: Paint House
- 문제 3: Paint House II
- 문제 4: Paint House III
- 문제 5: Count Vowels Permutation
- 문제 6: Number of Dice Rolls With Target Sum
정리
시작
이전 글에서 다이나믹 프로그래밍 문제풀이 전략에 대해 배웠습니다.
문제 풀이에 들어가기 전에 이전에 배운 내용을 정리해 봅시다.
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
완전탐색으로 해결 가능할 것 같은데 최솟값, 최댓값 혹은 경우의 수를 찾는 문제라면
다이나믹 프로그래밍 문제일 확률이 높습니다.
2. MEMO시 사용할 DP 테이블의 변수 정하기
어떤 변수를 사용하여 DP테이블을 구성할지 생각을 해야 합니다.
우리가 원하는 DP모양은 DP [I][J][K] = VALUE의 형태입니다.
VAULE에 해당하는 값은 I, J, K까지 진행하였을 때 최솟값, 최댓값, 혹은 경우의 수를 나타냅니다.
이러한 상황 속에서 최소한의 변수의 수, 구현이 간단한 변수를 찾아야 합니다.
3.DP의 RECURCE RELATION 찾기
문제의 예시를 기본으로 하여 점화식을 찾아야 합니다.
4. 부분 문제를 탐색 가능한 알고리즘 정하기(for loop, BFS, dfs, recurr etc...)
모든 부분 문제를 탐색 가능하고 구현하기 쉬운 알고리즘을 이용하여 구현하면 됩니다.
대부분 기초 dp문제에서는 for loop를 이용하여 구현하면 편한 문제가 대부분입니다.
5. 구현하기
위에서 정리한 내용을 바탕으로 구현합시다.
NOTE
초보자 분들은 1번에서 4번까지 종이를 사용하여 문제를 정리하고 마지막 5번에서 코드를 작성하는 것을 추천드립니다.
만약 생각을 코드로 바로 작성하게 된다면 코드 작성을 작성하는 일과 문제의 풀이를 생각하는 일 두 가지의 일을 같이하게 됩니다. 그러다 보면 뇌정지가 오고 문제를 틀리게 됩니다.
NOTE
dp = 완전탐색 + memo란 사실을 꼭 기억합시다.
매트릭스에서 DP
메트릭스에서 DP문제는 비교적 직관적입니다.
또한 DP문제 해결할 때 그림을 그리면 편한데 문제의 인풋으로 주어진 매트릭스를 이용하여 자연스럽게 분석하게 됩니다. 이번 챕터에서는 그림을 통해 DP문제를 분석하는 방법에 대해 집중적으로 연습해 봅시다.
문제 1 : 최소비용으로 목적지까지 도달하기
M*N 크기를 가지는 지도가 인풋으로 들어옵니다.
지도의 각 칸마다 자연수가 들어 있습니다.
자동차를 가지고 출발지 (0,0)에서 도착지 (M-1, N-1)로 이동하려 합니다.
자동차는 상하좌우로 이동 가능하며 이동시 지도의 칸에 존재하는 자연수만큼 비용이 소모됩니다.
이때 가장 적은 비용이 소모되는 경로와 그 비용을 리턴하세요.
예를 들어 아래와 같은 지도가 있다고 생각을 해봅시다.
| 1 | 2 |
| 3 | 1 |
자동차가 한번 방문 한 곳을 다시 방문하지 않고 출발지에서 도착지로 이동하는 방법은 2가지입니다.
NOTE
왜? 2가지일까요?
2가지가 나온 이유는 한번 방문한 지역을 다시 방문할 필요가 없기 때문입니다.
만약 임의의 지역을 여러 번 방문하게 되면 한번 방문한 방법보다 무조건 크거나 같습니다.
2번을 통과하는 경우 비용은 4이고 3을 통과하는 경우 비용은 3입니다.
그래서 경로 [(0,0), (0,1), (1,1)]과 비용 4를 리턴하면 됩니다.
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
문제 지문에 최솟값을 구하라는 말이 있습니다.
또한 모든 경우의 경로를 다 고려해 보고 최솟값을 뽑으면 답을 구할 수 있을 듯합니다.
2.MEMO시 사용할 DP 테이블의 변수 정하기
변수를 정하기 위해 3*3 예시를 이용해봅시다.
| 3 | 23 | 3 |
| 3 | 3 | 2 |
| 13 | 2 | 3 |
(3,3) 지점으로 들어가는 방법은 바로 위인 (2,3)에서 들어가는 것과 왼쪽 (3,2)에서 들어가는 방법이 있습니다. 만약 (2,3)과 (3,2)까지 최소비용이 계산되어 있다고 생각을 한다면
(3,3)까지의 최소비용은 min( (2,3)까지 최소비용, (3,2)까지 최소비용) + 3이 됩니다.
그래서 dp [x의 위치][y의 위치] = (x, y)의 까지의 최소비용으로 생각하면 될듯합니다.
3.DP의 RECURCE RELATION 찾기
위의 예제에서(3,3)으로 들어가는 방향을 2곳이었습니다.
그럼 (2,2)는 어떨까요?
(2,2)로 들어오는 경우의 수는 상하좌우 4가지 경우가 있습니다.
하지만 오른쪽과 아래쪽은 고려할 필요가 없습니다.
왜 그런지 생각해 봅시다.

그림에서 보면 dp [1][1]은 dp [2][1]그리고 dp [1][2]보다 먼저 방문합니다.
그리고 한번 방문하면 다시는 방문할 필요가 없기 때문에 위쪽에서 들어오는 dp [0][1]과
왼쪽에서 들어오는 dp [1][0]만 고려하면 됩니다.
결국 점화식은 dp [x][y] = min( dp [x-1][y] , dp [x][y-1] ) + matrix [x][y]입니다.
4. 탐색 방법
위에서 그린 그림을 탐색할 수 있는 알고리즘을 선택하여야 합니다.
이 문제에서는 FOR LOOP혹은 재귀적인 방법을 이용한 탐색을 이용하면 간단하게 구할 수 있습니다.
또한 BFS, DFS알고리즘을 공부해본 적이 있다면,
위의 그림은 tree이고 bfs혹은 dfs로 탐색 가능하다는 사실을 알고 있을 것입니다.
우리의 경우 학습하는 목적이 있으니 모두 다 싹 다! 구현 봐야 합니다.
5. 구현 - for loop
점화식을 보면 x-1, y-1이 있습니다.
만약 for loop를 아래와 같이 진행하면 x = 0 혹은 y =0에서 -1 값이 나와 원하는 값이 나오지 못합니다.
for x in range(m):
for y in range(n):
dp[x][y] = min( dp[x-1][y] , dp[x][y-1] ) + matrix[x][y]그렇기 때문에 이 부분을 처리해주어야 합니다.
처리하는 방법은 2가지가 있습니다.

위의 그림을 보면 1번의 경우에는 x = 0, y = 0을 처리하기 위해 구석의 값을 무한대로 놓고 시작하는 모습입니다. 그럼 (0,0)의 기본값만 넣어주면 아래와 같은 for loop로 처리 가능합니다.
matrix = [
[3,23,3],
[3,3,2],
[13,2,3]
]
dp = [ [INF for _ in range(n+1)] for _ in range(m+1) ]
dp[1][1] = matrix[0][0]
for i in range(1, n+1):
for j in range(1, n+1):
dp[i][j] = min( dp[i-1][j], dp[i][j-1] ) + matrix[i-1][j-1]두 번째의 경우 base case를 모든 구석에 대해 진행하고 메인 루프로 들어가는 방법입니다.
matrix = [
[3,23,3],
[3,3,2],
[13,2,3]
]
dp = [ [INF for _ in range(n)] for _ in range(m) ]
#base case
dp[0][0] = matrix[0][0]
for j in range(1,n): dp[0][j] = dp[0][j-1] + matrix[0][j]
for i in range(1,m): dp[i][0] = dp[i-1][0] + matrix[i][0]
#메인 알고리즘
for i in range(1, n):
for j in range(1, n):
dp[i][j] = min( dp[i-1][j], dp[i][j-1] ) + matrix[i][j]효율성 측면에선 2번의 경우가 좋지만...
구현 측면에선 base case를 조금만 생각해도 되기에 1번이 좋습니다.
그래서 저의 경우에는 1번 방법을 선호하는 편입니다.
5. 구현 - 재귀적으로 구현, DFS
(0,0)을 시작 노드로 하는 DFS를 구현해도 되지만,
연습 삼아 마지막 (3,3)에서 내려오는 방법을 생각해 봅시다.
그러면 그림을 그려봅시다.

그림을 그려보면 i = 0 혹은 j = 0에서 재귀 탈출 조건임을 확인할 수 있습니다.
그러면 바로 구현해봅시다.
눈치가 빠르신 분들은 위에서 그림을 그리며 확인한 방식이 DFS의 작동방식과 동일하다는 것을 알 수 있습니다.
다음번 호출할 노드가 명확하여 visited를 사용하지 않았지만,
명확히 단방향 트리에서 DFS입니다.
matrix = [
[3,23,3],
[3,3,2],
[13,2,3]
]
def recurr(i,j,matrix,memo):
#탈출 조건
if (i,j) in memo: return memo[(i,j)]
if i == 0 or j == 0: return matrix[i][j]
#메인 알고리즘
a = recurr(i-1,j,matrix,memo)
b = recurr(i,j-1,matrix,memo)
memo[(i,j)] = min(a,b) + matrix[i][j]
return memo[(i,j)]5. 구현 - bfs로 구현
DFS로 구현하는 방식은 재귀적으로 탐색하는 방식과 동일했습니다.
하지만 for loop로 탐색하는 방식은 bfs와 다릅니다.
어떻게 구현할지 명확하게 정리하기 위해 위에서 사용한 그림을 가져와 봅시다.

이번 경우에도 다음 노드 탐색에 대해 명확합니다.
그래서 visited와 adj를 구현할 필요는 없습니다.
matrix = [
[3,23,3],
[3,3,2],
[13,2,3]
]
nexts = [[(0,0) ,matrix[0][0]]]
memo = {(i,j) : INF for i in range(len(matrix)) for j in range(len(matrix[0]))}
#층 별로 탐색한다.
while nexts:
dummy = []
#층에 존재하는 노드에 대하여 처리하는 부분
for n in nexts:
#작은 값으로 변환
if memo[n[0]] > n[1]: memo[n[0]] = n[1]
#다음 층 노드를 정리
for ele in [(1,0), (0,1)]:
nx, ny = n[0][0] + ele[0], n[0][1] + ele[1]
if 0 <= nx < len(matirx) and 0 <= ny < len(matirx[0]):
dummt.append([(nx1, ny1), memo[n[0]]+ matrix[nx1][ny1])
nexts = dummy
print(memo[(len(matrix)-1, len(matrix[0])-1)]문제 2: 공 낙하 실험
n*n크기의 matrix가 있습니다.
matrix의 각 격자에는 자연수가 적혀 저 있습니다.
이 matrix의 맨 위에서 공을 떨어 트릴 것입니다.
공은 바로 아래 밭으로 이동하거나 한 칸 아래의 왼쪽 그리고 오른쪽으로 이동할 수 있습니다.
공은 이동할 때마다 격자에 적힌 수만큼 에너지가 감소합니다.
공의 이동 경로중 가장 작은 에너지를 감소시키는 경로의 에너지 감소 값을 리턴하세요
예를 들어 아래와 같은 matrix가 있다고 가정해봅시다.
| 1 | 3 | 3 |
| 2 | 2 | 3 |
| 2 | 11 | 7 |
| 7 | 3 | 77 |
공이 낙하할 수 있는 위치는 맨 위의 줄의 (0,0), (0,1), (0,2)입니다.
만약 3번에서 출발하고 가장 에너지 감소가 작은 경로는 아래와 같습니다.
| 1 | 3 | 3 |
| 2 | 2 | 3 |
| 2 | 11 | 7 |
| 7 | 3 | 77 |
다른 경로도 있을 수도 있지만 위에 표시된 경로는 에너지 감소를 최소로 하는 경로중 1개입니다.
공의 모든 시작 위치를 고려했을 때 에너지를 최소로 하는 경로는 아래와 같습니다.
| 1 | 3 | 3 |
| 2 | 2 | 3 |
| 2 | 11 | 7 |
| 7 | 3 | 77 |
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
문제의 지문에서 가장 작은 값을 리턴해야 한다고 나와 있습니다.
또한 모든 가능한 경로를 확인해 보면 간단하게 답을 찾을 수 있을 것 같습니다.
다이내믹 프로그래밍 유형이라 의심하고 문제를 봅시다.
2. MEMO시 사용할 DP 테이블의 변수 정하기
이전에 해결한 문제와 비슷합니다.
dp [위치 x][위치 y] = 최소_에너지_감소 라 생각하고 점화식을 찾아봅시다.
3.DP의 RECURCE RELATION 찾기
문제에서 공의 이동 경로를 정해주었습니다.
참 친절한 문제입니다.
문제의 조건을 토대로 점화식을 만들어 보면,
dp [i][j] = min( dp [i-1][j], dp [i-1][j-1], dp [i-1][i+1]) +matrix [i][j]
로 생각할 수 있습니다.
4. 탐색 방법
첫째줄에서 어디를 선택하는지는 독립 적입니다.
그래서 첫째 줄에 대해 각각 탐색을 진행하고 결과를 취합하여 정답을 제출하여야 합니다.
이게 무슨 말인지 확인하기 위해 그림을 그려봅시다.
간결성을 위해 3줄까지만 진행합시다.

이 그래프에 대해 모든 경우를 탐색해야 합니다.
가장 간단한 경우는 BFS로 한 번에 처리하는 방법입니다.
for loop와 재귀적(DFS)로도 처리가 가능합니다.
5. 구현 - BFS
맨 위인 인덱스가 0인 줄부터 시작하여 맨 아래의 줄까지 탐색합니다.
탐색 시 이때까지 계산된 값을 함께 저장해 두었다가 사용합니다.
다시 말해서 정보는 위치 (i, j)와 memo에 기록된 최솟값 memo[(i, j)] + matrix [i][j]를 가지고 진행합니다.
matrix = [
[1,3,3],
[2,2,3],
[7,3,77]
]
INF = float('inf')
nexts = [ [(0,i) ,matrix[0][i]] for i in range(len(matrix[0])) ]
memo = {(i,j): INF for i in range(len(matrix)) for j in range(len(matrix[0]))}
while nexts:
dummy = []
for n in nexts:
if memo[n[0]] > n[1]: memo[n[0]] = n[1]
for ele in [(1,-1), (1,0), (1,+1)]:
nx1, ny2 = n[0][0] + ele[0], n[0][1] + ele[1]
if 0 <= nx1 < len(matrix) and 0 <= nx1 < len(matrix[0]):
dummy.append((nx1, nx2) , memo[n[0]]+matrix[nx1][nx2]])
nexts = dummy
print(memo)
---> 출력결과
{(0, 0): 1, (0, 1): 3, (0, 2): 3,
(1, 0): 3, (1, 1): 3, (1, 2): 6,
(2, 0): 10, (2, 1): 6, (2, 2): 80}
# 마지막 줄에서 최솟값 6을 리턴하면 정답이다.
5. 구현 - for loop
이번 문제의 경우도 이전 문제처럼 2가지 방법이 존재합니다.
dp테이블을 주어진 인풋 matrix의 크기와 같은 크기 만드는 방법과 크게 만드는 방법입니다.

1번 방법의 경우 dp테이블을 만들고 matrix의 첫쨰줄에 해당하는 값을 base case로 넣어 주어야 합니다.
하지만 2번의 경우는 dp테이블을 크게 만들고 모든 값을 0으로 초기화하여 진행하면 됩니다.
그럼 1번부터 구현해 봅시다.
matrix = [
[1,3,3],
[2,2,3],
[7,3,77]
]
dp = [[0 for i in range(len(matrix[0]))] for j in range(len(matrix))]
for i in range(len(matrix[0])):
dp[0][i] = matrix[0][i]
answer = float('inf')
for i in range(1,len(matrix)):
for j in range(len(matrix[0])):
dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i-1][j+1]) + matrix[i][j]
if i == len(matirx)-1 and answer > dp[i][j]: answer = dp[i][j]
print(answer)2번의 경우는
matrix = [
[1,3,3],
[2,2,3],
[7,3,77]
]
dp = [[0 for _ in range(len(matrix[0])+2)] for _ in range(len(matrix)+1)]
answer = float('inf')
for i in range(1,len(matrix)+1):
for j in range(1,len(matrix[0])+1):
dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i-1][j+1]) + matrix[i][j]
if i == len(matirx)-1 and answer > dp[i][j]: answer = dp[i][j]
print(answer)구현은 2번 방법이 쉬우나 dp 테이블을 만드는 곳에서 약간 비효율적입니다.
각각 장단점이 있지만 실전에서는 2번 방법을 사용하는 것을 추천드립니다.
5. 구현 - 재귀적으로 구현해 보기, DFS
재귀적으로 구현하기 위해 역으로 생각해봐야 합니다.
NOTE
DFS와 동일합니다.
그림을 그려봅시다.
그림의 간결성을 위해 3*3 matrix에서 진행해 봅시다.
상황에 대한 정확한 이해를 위해 꼭! 직접 그려봅시다.
그림을 그리면 아래와 같습니다.

문제에서 원하는 결과를 얻기 위해서는 matrix의 마지막 열에 존재하는 모든 성분에 대해 조사를 해야 합니다.
하지만 위의 그림처럼 1번에서 계산된 dp(1,1)은 2번과 3번에서도 등장합니다.
이를 memo기법을 이용하여 처리하면 좋을 듯합니다.
리커션을 구현할 때 탈출 조건도 명확하게 생각하고 들어가야 합니다.
위의 그림에서 보면 dp(i, j)가 i == 0이면 matrix [i][j]를 리턴해야 합니다.
또한 memo에 (i, j)가 기록되어 있으면 리턴해야 합니다.
그러면 구현해 봅시다.
matrix = [
[1,3,3],
[2,2,3],
[7,3,77]
]
def dp(i,j, matrix, memo):
if (i,j) in memo: return memo[(i,j)]
if i == 0: return matrix[0][j]
ans = float('inf')
for n in [-1,0,1]:
ans = min( ans, dp(i-1,j-n, matrix, memo) )
memo[(i,j)] = ans + matrix[i][j]
return memo[(i,j)]
answer = []
for i in rangep(len(matrix[0])):
answer.append(dp(len(matrix), i))
print(min(answer))문제 3 : [카카오 인턴] 경주로 건설
https://programmers.co.kr/learn/courses/30/lessons/67259%EF%BB%BF
코딩테스트 연습 - 경주로 건설
[[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] 3800 [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] 2100 [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
최소 비용을 계산하는 문제입니다.
또한 모든 경우를 고려하였을 때 가능할 듯합니다.
dp유형을 의심해 봅시다.
2.MEMO시 사용할 DP 테이블의 변수 정하기
이 문제의 경우 1번 문제에 코너수에 가격 측정이 추가되었습니다.
1번 문제에서는 'dp [x][y] = 최소비용'을 나타내는 테이블을 이용했습니다.
1번 문제에서 정의한 테이블에 코너수에 대한 변수를 추가하여 생각해 봅시다.
그래서 'dp [x][y][코너수] = 최소 비용'으로 생각합시다.
위처럼 생각하고 진행해도 되지만,
dp [x][y][방향 = 상하좌우] = 최소 비용 일 때를 생각해 봅시다.
코너가 생성되기 위해 서는 방향 전환이 필요합니다.
코너수보다는 좀 더 기본적인 방향을 고려하여 진행하여 봅시다.
NOTE
dp [x][y][코너수] = 최소 비용도 생각하여도 문제 해결이 가능합니다.
3.DP의 RECURCE RELATION 찾기
dp [x][y][방향]의 최소 비용을 구할 수 있는 점화식을 구해봅시다.
dp [x][y][방향]로 갈 수 있는 이전 상태는 상하좌우에서 진입하는 경우 * (방향이 변하는 경우 or 방향이 변하지 않는 경우 )로 나눌 수 있습니다.
4가지 방향 중 왼쪽에서 들어오는 경우 점화식은 아래와 같습니다.
dp [i][j][right] = min(
dp [i][j-1][right] + 100,
dp [i][j-1][left] + 600,
dp [i][j-1][up] + 600,
dp [i][j-1][down] + 600
)
4. 변수 인덱스의 범위를 명확히 정리하기와 구현
이런 board에서 최단 거리 문제를 풀 때는 BFS로 해결하는 것이 깔끔합니다.
원리상 모든 노트를 탐색하며 dp를 업데이트하면 무슨 구현이든 상관이 없지만,
BFS로 구현 시 가장 직관적이고 효육적인 코드를 구현할 확률이 높습니다.
5. 구현 - BFS
BFS를 구현 시 생각해 봐야 할 부분은 이웃한 노드를 탐색할지를 결정하는 부분입니다.
기본적인 BFS에서는 visited를 이용하여 구현하였습니다.
vsited를 이용하여 탐색하는 노드의 이웃 노드들에 대하여 다음번에 탐색을 진행할지를 결정하였습니다.
만약 이웃 노드가 한번 탐색되어 visited에 처리되었다면,
이웃 노드라 할지라도 다음번에 탐색을 진행하지 않았습니다.
이번 문제에서는 기존의 visited방식을 수정하여야 합니다.
무슨 이야기 인지 확인하기 위해 아래의 그림을 봅시다.
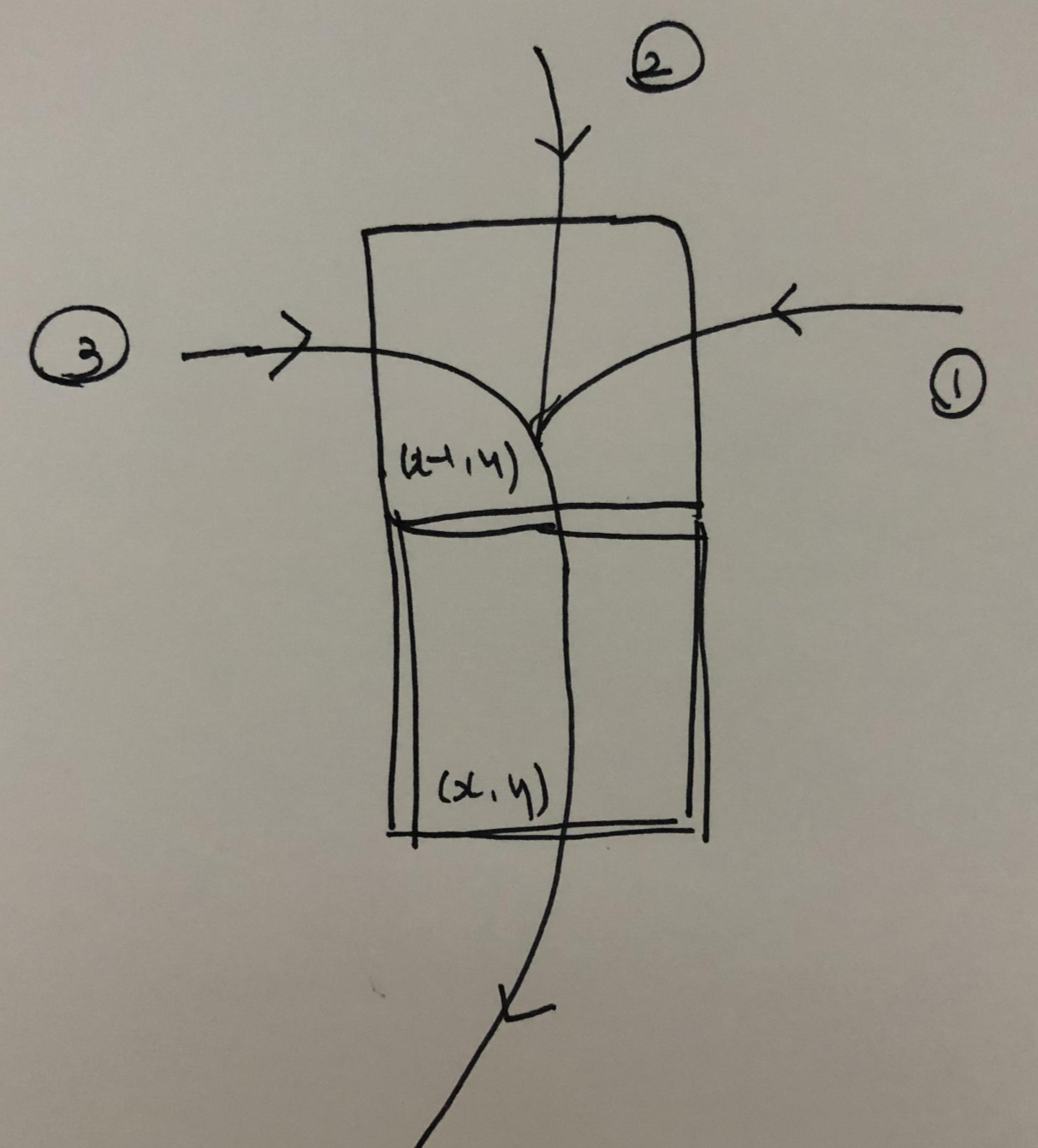
그림의 상황은 대략적으로 이렇습니다.
1번 경로가 (x, y, d)를 통과하여 INF에서 c로 dp가 패치된 상황입니다.
차후에 2번과 3번 경로가 (x, y, d) 상태를 지날 가능성이 있습니다.
만약 2번과 3번 중 계산된 값이 1번 경로로 인해 변경된 값인 c보다 작다면,
(x, y, c)를 다음 노드로 추가하고 탐색을 진행해야 할 것입니다.
이를 대략적인 코드로 나타내면 아래와 같습니다.
while nexts:
dummy = []
....
....
....
....
....
if dp[x][y][o] > new_c:
dp[x][y][o] = new_c
dummy.append(x, y, o, c)
nexts = dummy
위의 결과를 적용하여 구현하면 아래와 같이 구현할 수 있습니다.
def solution(board):
w = len(board)
INF = float('inf')
dp = [ [ {'r': INF, 'l': INF, 'u':INF, 'd':INF} for _ in range(w)] for _ in range(w)]
moves = {(0,1) : 'r', (0,-1):'l', (1,0):'d', (-1,0):'u'}
nexts = [(0,0,ori,0) for ori in moves.values()]
#base case
for x, y, o, c in nexts:
dp[x][y][o] = c
#BFS를 이용한 그래프 탐색
while nexts:
dummy = []
for x, y, o, c in nexts:
for m in moves.keys():
nx, ny, no = x+m[0], y+m[1], moves[m]
nc = c + 100 if o == no else c + 600
#탐색 좌표 범위 확인
if 0 <= nx < w and 0 <= ny < w:
#벽 확인
if board[nx][ny] == 1: continue
#다음 노드 추가, dp 업데이트
if dp[nx][ny][no] > nc:
dp[nx][ny][no] = nc
dummy.append((nx, ny, no, nc))
nexts = dummy
return min(dp[-1][-1].values())5. 구현 - DFS(재귀)
이번 구현은 11,12,19번이 시간 초과 판정을 받습니다.
또한 리커션 리밋을 아래의 코드와 같이 수정해 주지 않으면 12번이 런타임 에러 판정을 받습니다.
단지 깊이 우선으로 그래프를 탐색하였는데 많은 시간이 차이가 납니다.
import sys
x = 9999999
sys.setrecursionlimit(x)
moves = [(0,1), (0,-1), (1,0), (-1,0)]
direc = {(0,1) : 'r', (0,-1): 'l', (1,0):'u', (-1,0): "d"}
op = {'r':'l', 'd':'u', 'l':'r', 'u':'d'}
def solution(board):
INF = float('inf')
dp = [ [ {'r': INF, 'l':INF, 'u':INF, 'd':INF} for _ in range(len(board))] for _ in range(len(board))]
dp[0][0] = {'r': 0, 'l': 0, 'u':0, 'd':0}
global op
for ele in op.keys():
dfs(0, 0, ele, 0, dp, board)
return min(dp[-1][-1].values())
def dfs(x, y, o, cost, dp, board):
if dp[x][y][o] < cost: return
dp[x][y][o] = cost
global moves, direc, op
for move in moves:
nx, ny, no = x + move[0], y + move[1], direc[move]
ncost = cost + 100 if no == o else cost + 600
if op[o] != no and 0 <= nx < len(board) and 0 <= ny < len(board) and board[nx][ny] == 0:
dfs(nx, ny, no, ncost, dp, board)
5. 구현 - For loop
처음 알고리즘을 구현하면 대부분 아래와 같이 구현합니다.
N = len(board)
INF = float('inf')
dp = [[[INF for i in range(4)] for j in range(N)] for k in range(N)]
dp[0][0] = [0, 0, 0, 0]
for r in range(N):
for c in range(N):
if r-1>-1 and board[r-1][c]==0:
dp[r-1][c][1] = min(dp[r-1][c][1], dp[r][c][0]+600,
dp[r][c][1]+100, dp[r][c][2]+600, dp[r][c][3]+600)
if r+1<N and board[r+1][c]==0:
dp[r+1][c][0] = min(dp[r+1][c][0], dp[r][c][0]+100,
dp[r][c][1]+600, dp[r][c][2]+600, dp[r][c][3]+600)
if c-1>-1 and board[r][c-1]==0:
dp[r][c-1][3] = min(dp[r][c-1][3], dp[r][c][0]+600,
dp[r][c][1]+600, dp[r][c][2]+600, dp[r][c][3]+100)
if c+1<N and board[r][c+1]==0:
dp[r][c+1][2] = min(dp[r][c+1][2], dp[r][c][0]+600,
dp[r][c][1]+600, dp[r][c][2]+100, dp[r][c][3]+600)하지만 위의 알고리즘은 정답 판정을 받을 수 없습니다.
그 이유에 대해 분석해 봅시다.
정답 판정을 받지 못한 이유는 board에 존재하는 벽 때문입니다.
이에 대한 감을 익히기 위해 아래의 예제를 봅시다.
색칠된 곳은 벽이고, 빈칸은 도로 건설 가능 지역입니다.

위의 경우 s에서 e로 가는 경로는 단 1개뿐입니다.
이 경로의 비용이 경주로를 건설하는데 최소 비용이 될 것입니다.
이 board에 대해서 아래와 같은 loop를 처리해 봅시다.

위의 그림은 for loop가 끝나고 최저 비용이 처리된 곳을 동그라미로 표시하고,
아무런 업데이트가 되지 않은 곳을 엑스로 표시하였습니다.
이 그림을 보면 탐색 순서 때문에 처리되지 않은 곳이 생깁니다.
그럼 dp는 초기화하지 않은 상태에서 for loop로 구현된 알고리즘을 1번 더 돌리면 어떻게 될까요?

검은색 동그라미 부분까지 최소 비용이 계산됩니다.
결국 위로 올라가야 하고 벽으로 인해 탐색되지 않는 곳까지 전부 탐색하기 위해서는 for loop를 여러 번 돌려야 합니다. 최대 칸의 수만큼 for loop를 진행하게 되면 모든 경우를 다 탐색이 가능할 것입니다.
그러니 for _ in range(N*N)을 코드에 추가해 줍시다.
def solution(board):
N = len(board)
INF = float('inf')
dp = [[[INF for i in range(4)] for j in range(N)] for k in range(N)]
dp[0][0] = [0, 0, 0, 0]
for _ in range(N*N):
for r in range(N):
for c in range(N):
if r-1>-1 and board[r-1][c]==0:
dp[r-1][c][1] = min(dp[r-1][c][1], dp[r][c][0]+600,
dp[r][c][1]+100, dp[r][c][2]+600, dp[r][c][3]+600)
if r+1<N and board[r+1][c]==0:
dp[r+1][c][0] = min(dp[r+1][c][0], dp[r][c][0]+100,
dp[r][c][1]+600, dp[r][c][2]+600, dp[r][c][3]+600)
if c-1>-1 and board[r][c-1]==0:
dp[r][c-1][3] = min(dp[r][c-1][3], dp[r][c][0]+600,
dp[r][c][1]+600, dp[r][c][2]+600, dp[r][c][3]+100)
if c+1<N and board[r][c+1]==0:
dp[r][c+1][2] = min(dp[r][c+1][2], dp[r][c][0]+600,
dp[r][c][1]+600, dp[r][c][2]+100, dp[r][c][3]+600)
return min(dp[N-1][N-1])연속된 부분 처리하는 유형
연속된 부분을 찾거나 부분 수열을 찾는 문제는 dp로 해결 가능합니다.
연속된 부분 처리방법을 익혀봅시다.
문제 1 : 증가하는 가장 큰 수열 만들기
인풋으로 자연수로 구성된 리스트 nums가 주어집니다.
인풋에 대해 성분의 순서는 바꿀 수는 없지만, 임의의 위치에 있는 성분을 마음대로 제거할 수 있습니다.
이 조건으로 만들 수 있는 리스트 중에 가장 긴 증가 하는 수열의 길이를 리턴하세요.
예를 들어
nums = [ 9, 9, 9, 1, 2, 3, 4, 5 ,6 ]이 인풋으로 들어온다면,
가장 긴 증가하는 수열은 [1, 2, 3, 4, 5 ,6]입니다.
nums = [9, 9, 2, 5, 3, 7, 77, 77]
이 인풋으로 들어온다면,
가장 긴 증가하는 수열은 [2, 3, 7, 77] 또는 [2, 5, 7, 77]입니다.
nums = [77, 77]
이 인풋으로 들어온다면,
가장 긴 증가하는 수열은 [77]입니다.
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
성분을 제거하여 만들 수 있는 모든 수열을 완전 탐색으로 해결 가능할 것 같습니다.
또한 가장 긴 증가 하는 수열의 길이를 찾아야 하므로 dp문제라 의심할 수 있습니다.
2.MEMO시 사용할 DP 테이블의 변수 정하기
테이블의 변수를 정하는 감을 익히기 위해 그림을 그려봅시다.
nums = [ 9, 9, 9, 1, 2, 3, 4, 5 ,6 ]에 대하여 index i번째 까지 모든 증가하는 수열을 찾는 과정을 생각해 봅시다.

위의 그림에서 index 6에서 모든 증가수열을 찾는 방법에 대해 분석해 봅시다.
index 6을 진행하기 전 index 5까지 모든 증가하는 수열을 찾은 상태입니다.
그럼 6까지의 모든 증가수열은
1-5번 까지 증가수열에 + nums [6]
으로 구할 수 있습니다.
하지만 그림에서 보면 5 ,4 ,3번 index에 대해서만 추가가 되었습니다.
1, 2번의 경우 증가수열의 마지막 성분이(위의 예제에서 9입니다.) nums [6]보다 큽니다.
더 이상 증가 수열이 아닙니다.
결국 dp [index] = set(
increasing arrays
)로 나타내면 될듯합니다.
여기서 좀 더 업그레이드를 해봅시다.
우리가 원하는 값은 증가하는 수열 중 가장 큰 값입니다.
그럼 dp [index] = length_longest_increasing_array 요런 식으로 표현 가능하지 않을까요?
이를 분석해 보기 위해 다시 그림을 그려봅시다.

6번의 경우 nums [i] < nums [6]를 만족하는 i에 대해
length [6] = max( nums [i] + 1 ) i = 3 ,4 ,5의 점화식을 계산되고 있습니다.
3.DP의 RECURCE RELATION 찾기
위에서 분석한 예제를 일반화하여
dp [index] = length_longest_increasing_array에 대해서 점화식을 생각해 보면
dp [index] = max( dp [i] + 1 )를 만족합니다.
여기서 i < index와 nums [index] > nums [i]를 만족하는 모든 i입니다.
4. 탐색 방법
1차원 문제라 for loop와 BFS는 탐색 방식이 같습니다.
그러니 for loop와 재귀적인 방법을 구현해 봅시다.
5. 구현 - for loop
위에서 예제를 분석한 방식을 그대로 구현하면 쉽게 가능합니다.
def Solution(nums: List[int]) -> int:
l = len(nums)
if l == 1: return 1
dp = [0 for _ in range(l)]
dp[0] = 1
for i in range(1, l):
next_ = 1
for j in range(i-1, -1, -1):
if nums[j] < nums[i]:
next_ = max(next_, dp[j] + 1)
dp[i] = next_
return max(dp)
5. 구현 - 재귀적으로 구현
재귀적으로 구현하기 위해 graph가 어떤 형태인지 명확하게 합시다.
아래의 그림은 dp [i]를 구하기 위해 graph를 그린 것입니다.

dp(i)를 구하기 위해 nums [i] > nums [j] and i > j를 만족하는 dp(j)를 호출합니다.
호출된 상태를 나타낸 위의 그림을 보면 dp(2)가 반복적으로 나타나는 것을 볼 수 있습니다.
이를 memo에 저장하였다 사용하면 될듯합니다.
또한 위에서 탐색할 j 중 작은 값부터 탐색을 하게 된다면 memo에 작은 값부터 저장이 되어 깔끔하게 진행될 듯합니다.
nums = [ 9, 9, 9, 1, 2, 3, 4, 5 ,6 ]
def recurr(i,memo):
if i in memo: return memo[i]
global nums
dummy = []
for j in range(i-1, -1, -1):
if nums[j] < nums[i]:
dummy.append(recurr(j, memo)+1)
memo[i] = max(dummy)
return memo[i]
memo = {1:1}
recurr(len(nums)-1,memo)
print(max(memo.values()))문제 2 : 최장 공통부분 수열
문자열 text1, text2가 인풋으로 주어질 때,
두 문자열에 대한 최장 공통부분 수열의 길이를 찾아 리턴하세요.
여기서 최장 공통부분 수열이란
text1으로 만들 수 있는 부분 수열의 집합 A와
text2으로 만들 수 있는 부분 수열의 집합 B의
교집합 중 가장 길이가 긴 성분을 말합니다.
예를 들어 text1="abbc", text2="bbb"라 하면
text1의 부분 수열 A = {a, b, c, ab, ac, bc, bb, abc, bbc}
text2의 부분 수열 B = {b, bb, bb}
공통부분 수열 A n B = {b, bb}
최장 부분 수열 = bb
이고 bb의 길이인 2를 리턴하면 됩니다.
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
text1의 모든 부분 수열과 text2의 모든 부분 수열을 정말 탐색하여 답을 구할 수 있고
문제에서 최장 부분 수열을 구하라고 나와 있습니다.
dp를 의심해 봅시다.
2. MEMO시 사용할 DP 테이블의 변수 정하기
문제에서 주어진 text1과 text2에 대해서 인덱스를 처리해야 합니다.
그래서 dp [text_1_index][text_2_index] = 최장 부분 수열이라 가정하고 생각해 봅시다.
가정에 대한 감을 익히기 위해 text1 = 'ab', text2 = 'bb'의 경우에 대해 그림을 그려봅시다.
dp의 변수가 text1, text2의 index입니다.
그러면 우리는 가로, 세로축이 각각 text1, text2인 테이블을 그려 확인할 수 있습니다.
| text1[0] = a | text1[1] = b | |
| text2[0] = b | dp[0][0] | dp[1][0] |
| text2[1] = b | dp[0][1] | dp[1][1] |
위에서 dp [i][j]은 text1 [:i+1], text2 [:j+1]에 대한 최장 부분 수열을 나타냅니다.
표를 하나씩 채워봅시다.
dp [0][0]은 text1 [0]!= text2 [0] 이므로 None입니다.
dp [1][0]은 text1 [1] == text2 [0] 이므로 b입니다.
dp [0][1]은 text1 [0]!= text2 [1] 이므로 None입니다.
dp [1][1]은 text1 [1] == text2 [1] 이므로 dp [0][0] + b입니다.
dp [1][1]에 대해 조금 더 생각해 봅시다.

위의 그림을 보면 좀 더 직관적으로 점화식을 이해할 수 있습니다.
만약 다음번 text1 [i] == text [j]의 성분이 같으면 dp [i-1][j-1] + 1을 해주면 됩니다.
3. DP의 RECURCE RELATION 찾기
예제의 경험을 일반화하여 점화식을 찾기 위해 좀 더 어려운 예제에 대해 분석해 봅시다.
text1 = "kakao", text2 = "aao"인 경우입니다.

위의 그림은 text1 [:i] (i = 1, 2, 3, 4, 5)와 text2 [0]에 대한 최장 공통부분 수열을 나타냅니다.
위의 표를 채우다 보면 1가지 패턴을 발견할 수 있습니다.
text1 [1] == text2 [0] == a인 지점 이후에 모드 a가 채워져야 합니다.
그럼 다음 줄을 채워 봅시다.

dp [1][0]은 text1 [0]!= text2 [1] 이므로 None입니다.
dp [1][1]은 text1 [1] == text2 [1] 이므로 dp [0][0] + a입니다.
dp [1][2]은 text1 [2] =! text2 [1] 이므로 이전 상태 dp [1][1]. dp [0][2]중 길이가 큰 값 a입니다.
dp [1][3]은 text2 [3] == text2 [1] 이므로 dp [0][2] + a입니다.
dp [1][4]은 text1 [4] =! text2 [1] 이므로 이전 상태 dp [1][3]. dp [0][3]중 길이가 큰 값 aa입니다.
이 패턴대로 맨 아래의 줄도 채워 봅시다.

이 경험을 일반화해보면 점화식은
if text1 [i] == test2 [j]:
dp [i][j] = dp [i-1][j-1] +1
else:
dp [i][j] = 길이가_가장_긴_것( dp [i-1][j], dp [i][j-1] )
요런 식으로 생각할 수 있습니다.
4. 탐색 방법
이전까지 for loop의 탐색 방법으로 예제를 분석하였습니다.
dp [i][j]를 탐색 시 왼쪽, 위쪽, 대각선 왼쪽 위에서 결과가 내려옵니다.
이런 형태의 구조에서는 BFS탐색으로 깔끔하게 해결할 수 있습니다.
재귀적인 방식도 당연히 해결 가능하니 for, bfs, 재귀 3가지로 구현해 봅시다.
5. 구현 - for loop
이전까지 분석한 내용을 고대로 구현해 봅시다.
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
l1 = len(text1)
l2 = len(text2)
dp = [ [0 for _ in range(l2+1)] for _ in range(l1+1)]
for i in range(1,l1+1):
for j in range(1, l2+1):
if text1[i-1] == text2[j-1]: dp[i][j] = dp[i-1][j-1] + 1
else: dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
text1 = "kakao"
text2 = "aao"
result = longestCommonSubsequence(text1, text2)
print(result)
5. 구현 - 재귀적으로 구현
재귀 구현을 위해 한 번 더 그림으로 확인합시다.

dp(i, j)는 text1 [i-1] == text2 [j-1] 경우와 text1 [i-1]!= text2 [j-1] 경우로 나누어 생각을 해야 합니다.
위의 그림에서 text1 [i-1] == text2 [j-1]인 경우 dp(i-1, j-1)을 호출하고,
text1 [i-1] == text2 [j-1]인 경우 dp(i, j-1), dp(i-1, j)를 호출하고 있습니다.
그림에는 나타내지 않았지만 dp(i-1, j-1)은 오른쪽의 다음번 호출에서 나올 것입니다.
이에 대해 명확하지 않다면 직접 그림을 그려봅시다.
어찌 되었건 dp(i-1, i-1)은 반복돼서 그래프에 표현될 것입니다.
이를 memo기법으로 효율적으로 처리합시다.
def dp(i, j, text1, text2, memo):
if (i,j) in memo: return memo[(i,j)]
elif text1[i] == text2[j]:
temp = dp(i-1, j-1, text1, text2, memo)
memo[(i,j)] = temp + 1
return memo[(i,j)]
else:
temp = 0
temp = max(0, dp(i, j-1, text1, text2, memo),
dp(i-1, j, text1, text2, memo))
memo[(i,j)] = temp
return memo[(i,j)]
memo = {}
#base case
if text1[0] == text2[0]: memo[(0,0)] = 1
else: memo[(0,0)] = 0
for i in range(1, len(text1)):
if memo[(i-1,0)] == 1 or text1[i] == text2[0]: memo[(i,0)] = 1
else: memo[(i,0)] = 0
for j in range(1, len(text2)):
if memo[(0,j-1)] == 1 or text1[0] == text2[j]: memo[(0,j)] = 1
else: memo[(0,j)] = 0
#main alogoritm
result = dp(len(text1)-1, len(text2)-1, text1, text2, memo)5. 구현 - BFS로 구현
재귀 구현을 위해 한 번 더 그림으로 확인합시다.
아래의 그림은 탐색 순서를 나타내었습니다.

탐색 순서를 보면 dp(i, j)를 탐색하자 할 때 필요한 dp(i-1, i-1), dp(i, i-1), dp(i-1, i) 모두 계산된 상태인 것을 확인할 수 있습니다. 그리고 한번 방문 시 최적의 해를 구할 수 있으므로 visited를 이용하여 한번 방문한 곳은 다시 방문하지 않도록 처리하면 됩니다.
그럼 이를 구현해 봅시다.
text1 = "kakao"
text2 = "aao"
l1 = len(text1)
l2 = len(text2)
dp = [ [0 for _ in range(l2 + 1)] for _ in range(l1 + 1)]
nexts = {(1,1)}
visited = [ [False for _ in range(l2 + 1)] for _ in range(l1 + 1)]
for i in range(l1+1): visited[i][0] = True
for j in range(l2+1): visited[0][j] = True
moves = [(1,0), (0,1)]
while nexts:
for i, j in nexts:
visited[i][j] = True
if text1[i-1] == text2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
dummy = set()
for i, j in nexts:
for m in moves:
ni, nj = i + m[0], j + m[1]
if 0<=ni<l1+1 and 0<=nj<l2+1 and visited[ni][nj] == False:
dummy.add((ni,nj))
nexts = dummy
return dp[-1][-1]여기서 조심해야 할 부분이 있습니다.
이전까지 풀이에서는 nexts의 자료구조로 리스트를 사용하였습니다.
하지만 여기서는 집합 자료구조를 사용하였습니다.
집합을 사용하는 이유는 다음과 같습니다.
리스트의 경우 메모리에 데이터를 연속적으로 저장해야 합니다.
또한 리스트 생성 시 파이썬 내부적으로 초기 인풋 값 보다 조금 큰 공간을 만들어 사용합니다.
그래서 기존에 만든 리스트의 크기를 초과하는 양을 리스트에 append 하게 되면 리스트의 크기를 늘리는 연산을 내부적으로 진행해야 합니다. 이 연산으로 인해 많은 시간 소모를 발생해 간혹 알고리즘 문제에서 시간 초과 판정을 받을 수 있습니다. 하지만 집합의 경우 hash map자료구조를 이용한 구현을 사용하고 있어, 데이터를 저장할 때 추가하는 연산만 진행됩니다. 그러니 이제부터 집합 자료구조를 사용하여 BFS의 nexts를 구현합시다.
문제 3 : 두 리스트의 가장 긴 공통부분 찾기
문자열 nums1, nums2가 인풋으로 주어질 때,
두 리스트의 가장 긴 공통 수열을 찾아야 합니다.
여기서 공통부분이란 1번 리스트를 "("과 ")"로 잘라 부분을 선택했을 때,
잘린 부분이 text2에도 존재하는 부분을 말합니다.
공통부분의 길이를 리턴하세요.
예를 들어
nums1 = [1, 1, 3, 3 ,5, 5, 7 ,7]
nums2 = [7, 7, 6, ,6 3, 5 ,5, 3, 1]
nums1의 부분 중 (3, 5, 5)와
nums2의 (3, 5, 5)는 공통부분 중 가장 긴 것입니다.
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
모든 부분에 대해 완전 탐색을 진행하면 간단히 해결 가능하고,
가장 긴 공통부분을 찾으란 말이 있으니 dp를 의심해야 합니다.
2. MEMO시 사용할 DP 테이블의 변수 정하기
nums1과 nums2 둘을 고려해야 합니다.
dp [nums1_index][nums2_index] = 가장 긴 공통부분의 길이
라 생각하고 진행해 봅시다.
감을 잡기 위해 그림을 그려 보면

대각선에서 +1이 되어 내려오는 것을 확인할 수 있습니다.
3. DP의 RECURCE RELATION 찾기
위의 경험을 일반화해보면,
if nums1 [i] == nums [j]:
dp [i][j] = dp[i-1][j-1] +1
else:
dp[i][j] = 0
입니다.

4. 탐색 방법
이번 문제의 경우 BFS구현은 각자 해보도록 합시다.
for loop와 재귀적으로 구현해봅시다.
초기 조건의 편리성을 위해 아래와 같은 테이블에서 진행해봅시다.
5. 구현 - for loop
이전까지 분석한 내용을 고대로 구현해 봅시다.
l1 = len(nums1)
l2 = len(nums2)
dp = [ [0 for _ in range(l2+1)] for _ in range(l1+1)]
answer = 0
for i in range(1,l1+1):
for j in range(1,l2+1):
if nums1[i-1] == nums2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
if dp[i][j] > answer: answer = dp[i][j]
print(answer)
5. 구현 - 재귀적으로 구현
아래의 코드에서 m[(i, j)] = temp 쪽을 조심해야 합니다.
위의 for loop에서 대각선에서 내려오는 경우만 존재하고 n1 [i]!= n2 [j]이면 모두 0이었습니다.
이를 그대로 재귀적으로 구현하려면 m[(i, j)] = temp로 설정해야 합니다.
temp1과 temp2의 경우는 모든 경우를 탐색하기 위해서 존재합니다.
만약 temp1, temp2가 없으면 모든 경우를 탐색하지 않아 정답 판정을 받지 못합니다.
def dp(i, j, n1, n2, m):
if (i,j) in m: return m[(i,j)]
if i == 0 or j == 0: return 0
global answer
temp = 0
if n1[i-1] == n2[j-1]:
temp = dp(i-1,j-1,n1,n2,m) + 1
temp1 = dp(i-1, j, n1, n2, m)
temp2 = dp(i, j-1, n1, n2, m)
m[(i,j)] = temp
answer = max(temp1, temp, temp2, answer)
return m[(i,j)]
memo = {}
l1 = len(nums1)
l2 = len(nums2)
global answer
answer = 0
dp(l1, l2, nums1, nums2, memo)
print(answer)문제 4 : 복수전공 수강 신청
영희는 물리학과 컴퓨터 과학을 복수 전공하고 있습니다.
각 학과의 커리큘럼에는 선행 과목이란 개념이 존재합니다.
선행 과목이란 특정 과목을 수강하기 위해서는 필수적으로 수강해야 하는 과목을 의미합니다.
학과의 커리큘럼은 1차원 리스트에 저장되어있습니다.
1차원 리스트의 i번째 과목을 수강하기 위해서는 i-1번 과목을 반듯이 수강해야 합니다.
예를 들어 학과의 커리큘럼이 [a, e, r, r, c, k]로 주어진다면,
과목 e를 수강하기 위해서는 a를 반듯이 수강해야 합니다.
물리학 커리큘럼을 담은 리스트 p와 컴퓨터 과학의 커리큘럼을 담은 c 그리고 영희가 수강 신청한 리스트 s가 주어집니다. 이때 영희가 수강신청 리스트가 가능하면 True, 불가능하면 False를 리턴하는 함수를 만드세요.
단,
len(p) + len(c) = len(s)입니다.
과목은 알파벳 소문자 1개입니다.
예를 들어
p =[ m, p, a, a]
c= [ c, m, p, k, a]
s = [m, c, p, a, a, m, p, k, a]
s=[p [0], c [0], p [1], p [2], p [3], c [1], c [2], c [3], c [4] ]로 가능합니다.
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제인지 지문을 통해 힌트를 얻는다.
이번 문제는 최솟값 혹은 최댓값을 구하는 문제가 아닙니다.
하지만 dp문제입니다.
시간 순으로 처리를 해야 하거나 순차적으로 처리를 해야 하는 경우 dp를 의심해야 합니다.
이런 문제는 가능한 모든 수강신청의 경우의 수를 리턴하라는 문제로 나올 수도 있습니다.
2. MEMO시 사용할 DP 테이블의 변수 정하기
컴퓨터 과학과 물리학의 선행과목 조건을 충족해야 합니다.
그래서 dp [p_index][c_index] = 가능?으로 가정하고 예제를 분석해 봅시다.
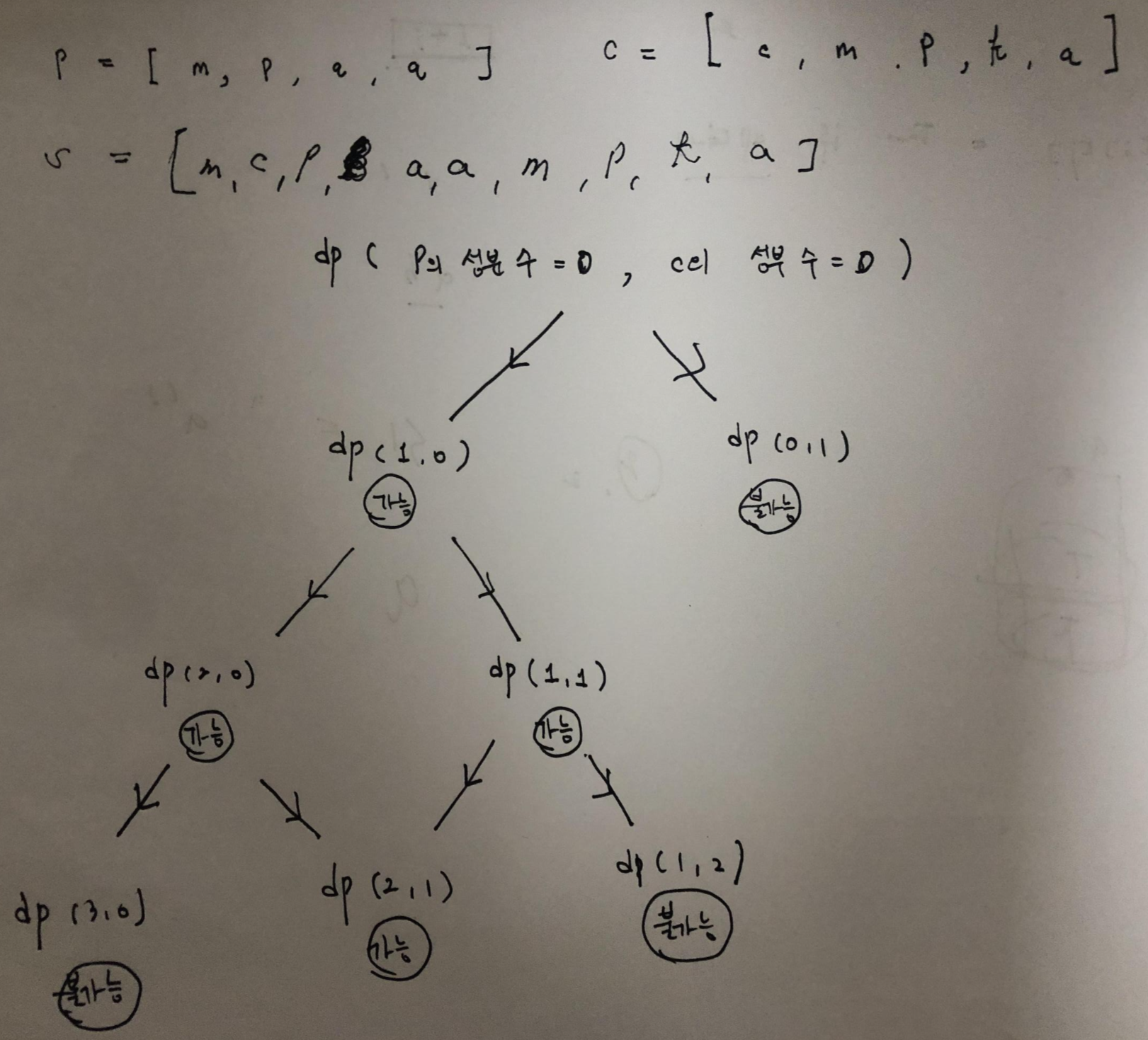
위의 그림에서 dp의 파라 매터는 각각 p의 성분의 수와 c의 성분의 수를 나타냅니다.
p의 성분의 수 + c의 성분의 수는 = s의 index로 생각할 수 있습니다.
예를 들어 dp(2,3)이라 해면 p 2개 c 3개 s 5개까지 확인한 상태입니다.
만약 p 2개와 c 3개로 s 5개를 만들 수 있다면, True를 리턴합니다.
s [0]는 p [0]이 선택될 수도 있고 c [0]가 선택될 수도 있습니다.
그래서 위의 그림에서 dp(0,0)이 d(1,0)과 dp(0,1)을 호출하고 있습니다.
3. DP의 RECURCE RELATION 찾기
위의 경험에서 점화식을 찾아보면 대략적으로 아래와 같습니다.
def psudeo_recurr(i, j):
if (i,j) in memo: return memo[(i,j)]
if p[i] == s[i+j]:
temp1 = dp(i+1, j)
if c[j] == s[i+j]:
temp2 = dp(i, j+1)
if temp1 or temp2: return True
else: return False
4. 탐색 방법
코드가 깔끔하게 작성할 수 있는 초기 조건과 탐색방법을 찾아봅시다.
재귀의 경우 dp(0,0)부터 탐색하게 된다면 초기 조건으로 아무것도 주지 않아도 됩니다.
5. 구현 - 재귀적으로 구현
엄청 간단하게 구현이 됩니다.
def dp(i,j,memo):
memo[(i,j)] = True
if i < len(s1):
if s1[i] == s3[i+j]:
dp(i+1,j,memo)
if j < len(s2):
if s2[j] == s3[i+j]:
dp(i,j+1,memo)
memo = {}
dp(0,0,memo)
if (len(s1), len(s2)) in memo: return True
else: False5. 구현 - for loop
for loop의 base case를 설정을 위해 그림을 그려봅시다.
(데스크톱_이용 시_추가_준비 중)
l1, l2 = len(s1), len(s2)
dp = [ [False for _ in range(l2+1)] for _ in range(l1+1)]
dp[0][0] = True
'''
for i in range(1,l1+1):
if dp[i-1][0] == True and s1[i-1] == s3[i-1]:
dp[i][0] = True
for j in range(1,l2+1):
if dp[0][j-1] == True and s2[j-1] == s3[j-1]:
dp[0][j] = True
'''
for i in range(l1+1):
for j in range(l2+1):
if i == 0 and j == 0: continue
if 0<= i+j-1 <l1+l2 and 0 <= i-1:
if s1[i-1] == s3[i+j-1] and dp[i-1][j]: dp[i][j] =True
if 0<= i+j-1 <l1+l2 and 0 <= j-1:
if s2[j-1] == s3[i+j-1] and dp[i][j-1]: dp[i][j] =True
print( dp[l1][l2] )문제 4 : [카카오 인턴] 보석 쇼핑
https://programmers.co.kr/learn/courses/30/lessons/67258
코딩테스트 연습 - 보석 쇼핑
["DIA", "RUBY", "RUBY", "DIA", "DIA", "EMERALD", "SAPPHIRE", "DIA"] [3, 7]
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
완전 탐색으로 풀 수 있을 것 같고, 가장 짧은 구간을 찾는 문제입니다.
dp를 의심해 봅시다.
2. MEMO시 사용할 DP 테이블의 변수 정하기
구간을 구해야 합니다.
그래서 시작 인덱스와 끝 인덱스를 변수로 생각해 봅시다.
문제에서 원하는 조건이 i - j범위에 모든 종류의 보석이 들어 있는지 확인하는 문제입니다.
그러니 dp [i][j] = {보석 : 보석의 수}로 가정하고 생각해 봅시다.
예를 들어 gems = [a, b, b, a]에 대해서 생각해 봅시다.

위의 그림은 대략적으로 이렇습니다.
dp(0,3)은 가장 긴 구간을 나타냅니다.
모든 종류의 보석을 포함하고 있습니다.
그래서 구간을 줄일 수 있습니다.
앞에서 줄인 dp(1,3)과 뒤에서 줄인 dp(0,2)를 호출합니다.
만약 모든 종류의 보석을 포함하고 있지 않으면, 호출하지 않고 종료합니다.
3. DP의 RECURCE RELATION 찾기
위의 그림에 대한 점화식은 대략적으로 아래와 같습니다.
global answer
answer = float('inf')
def dp(i,j):
global answer
if answer > j-i+1: anser = j-i+1
if gems[i:j+1]이 모든 종류를 포함하면:
dp(i-1, j)
dp(i, j-1)
4. 탐색 방법
이번 문제의 경우 효율적인 탐색방법을 설계하고 들어가야 하는 문제입니다.
5. 구현 - DFS - 무지성
효율성은 일단 접어두고 재귀적으로 일단 구현해 봅시다.
보석의 종류를 알아보기 위해서 ps = { 보석 종류 : 개수 } 데이터 구조를 이용했습니다.
하지만 다음번 recurr 호출 시 ps를 복사하여 넘겨주고 있습니다.
이러한 구현은 시간 초과 판정을 받습니다.
문제를 잘 읽어 보면 보석의 종류는 대문자로 구성되었고 이름의 길이는 1에서 10 사이입니다.
최악의 경우 ps를 복사 시 O(24**10)의 시간 복잡도가 소요됩니다.
위의 그림에서 dp(1,2)가 반복되는 것을 확인하고 메모를 처리하였지만 탐색 방법과 구현이 비효율적이라 다른 방법을 찾아봐야 합니다.
def solution(gems):
max_leng = len(set(gems))
ps = {}
answer = []
visited = set()
for gem in gems:
if gem in ps: ps[gem] += 1
else: ps[gem] = 1
recurr(0, len(gems)-1, ps, max_leng, answer, gems, visited)
answer.sort(key = lambda x : (x[2],x[0]))
return answer[0][:2]
def recurr(i,j,ps,max_leng, answer, gems, visited):
if len(ps) == max_leng:
answer.append((i+1,j+1,j-i))
if i+1 <= j and i+1 >= 0 and (i+1, j) not in visited:
ps1 = ps.copy()
ps1[gems[i]] -= 1
if ps1[gems[i]] == 0: ps1.pop(gems[i])
recurr(i+1, j, ps1, max_leng, answer, gems, visited)
if i <= j-1 and i >= 0 and (i, j-1) not in visited:
ps2 = ps.copy()
ps2[gems[j]] -= 1
if ps2[gems[j]] == 0: ps2.pop(gems[j])
recurr(i, j-1, ps2, max_leng, answer, gems, visited)
6. 무지성 DFS 피드백
일단 위의 코드에 대해서 생각해 봅시다.
위의 구현에서 recurr(i, j) 다음으로 recurr(i+1, j)와 recurr(i, j-1)을 호출하고 있습니다.
호출 시 dictionary 자료구조인 ps를 넘겨주어 상태를 기록하고 있습니다.
여기서! ps를 복사하여 넘겨주어야 하는 상황이 발생합니다.
파이썬에서 dictionary는 리스트처럼 mutable 데이터 타입입니다.
만약 mutable이란 용어가 익숙하지 않으면 여기를 클릭해 주세요!
그래서 ps는 어느 함수에서나 공용으로 관리됩니다.
이해를 위해 예를 봅시다.
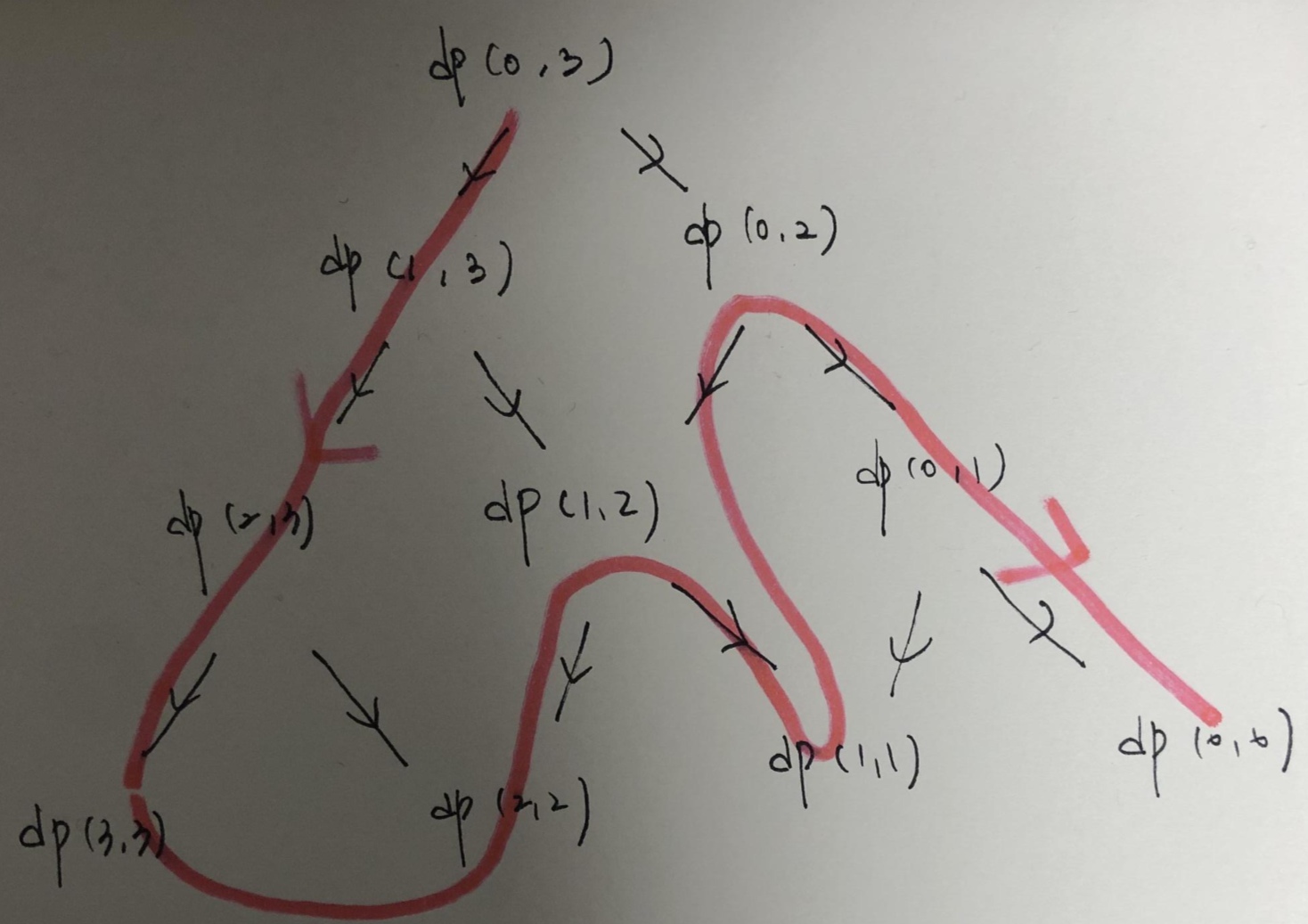
위의 그림에서 재귀적으로 호출을 하게 되면 빨간색을 따라 이동하면 탐색합니다.
여기서 dp(1,1) 다음으로 dp(0,2)가 호출됩니다.
이 부분에서 ps가 공통으로 관리되기 때문에 문제가 생깁니다.
dp(0,2)는 ps를 dp(0,3)에서 받아야 합니다.
하지만 dp(1,1)이 ps를 가공한 상태에서 dp(0,2)가 호출되기 때문에, ps.coy()를 이용하여 독립적인 값을 전단해야 합니다.
정답 판정을 받기 위해서는 ps.copy()를 하지 않고 구현하는 탐색 방법을 찾아야 합니다.
물론 ps를 dictionary 자료구조가 아닌 immutable 자료구조 중 하나인 string을 사용하여도 어느 정도는 해결이 가능할 듯합니다. 일단 탐색방법을 생각해 봅시다.
위의 그림에서 copy()를 사용하는 결정적인 이유는 dp(1,1)에서 dp(0,2)를 호출하는 상황 때문입니다.
만약 dp(1,1)이 dp(2,1), dp(1,2), dp(0,1), dp(1,0)과 같이 1만 차이나는 노드를 1개만 호출하게 된다면 copy()를 사용하지 않아도 됩니다.
위의 조건을 충족시키는 탐색 방법 중 알고 있는 알고리즘을 선택하면 됩니다.
BFS는 일단 아닙니다. DFS는 이전의 구현 방식과 동일합니다.
그러니 for loop로 생각해 봅시다.

이 그림은 dp(0,0)부터 시작하여 dp(3,3)까지 진행하는 2중 for loop의 탐색 경로를 나타낸 그림입니다.
그림에서 dp(0,3)에서 dp(1,1)로 이동하는 부분에서 ps를 다루기 까다롭습니다.
dp(0,0), dp(1,1), dp(2,2), dp(3,3)에서 새로운 ps를 만들어야 dp로 사용할 수 있습니다.
모든 구간에 해당하는 dp가 아니기에 좀 더 생각해 봅시다.
한 번에 copy() 없이 동작하는 경로를 찾아야 합니다.
뭔가 함정에 빠진 것 같고 경로를 못 찾겠으니 다시 처음으로 돌아가 봅시다.
예제 [a, b, a, b ]에 대해 ps 한 번으로 해결 가능한 방법을 생각해 봅시다.
note
ps가 한 번에 해결하기 위해서는 dp(i, j)에서 1칸만 움적 이여합니다.
예를 들어 dp(i-1,1), dp(i+1, j)등이 있습니다.

len(ps)!= 보석 종류 이면 dp [i][j]에서 dp[i][j+1]로 이동합니다.
len(ps) == 보석 종류 이면 dp[i][j]에서 dp [i+1][j]로 이동합니다.
이 방식으로 끝까지 탐색하면 됩니다.
이를 그래프로 표현해 보면,

이 그림과 같습니다.
dp [i][j]는 아래 왼쪽 혹은 아래 오른쪽으로 이동할 수 있습니다.
예제 [a, b, a, b]의 경우 빨간색 경로를 따라 이동합니다.
7. 점화식
위의 경험을 일반화시켜본다면, 점화식은 아래와 같습니다.
if len(ps) == 보석 종류: # dp[i][j] = ps
ps에 j+1번째 성분을 추가 # dp[i][j+1] = ps
다음번 탐색 노드를 (i, j+1)로 설정
else:
ps에 i번째 성분 제거 # dp[i+1][j] = ps
다음번 탐색 노드를 (i+1, j)로 설정
8. 구현- for loop
사실 이러한 구현 방식을 Two pointers 알고리즘이라 합니다.
이제 부터 1차원 리스트에 대한 탐색을 진행할 경우 BFS, DFS, 재귀, FOR LOOP, Two poinerts를 염두해 두고 탐색방법을 생각해봅시다.
이에 대해 조금 더 공부를 원한다면 여기를 클릭해 주세요.
def solution(gems):
num = len(set(gems))
ps = {gems[0]: 1}
next_ = (0,0)
answer = []
while next_:
start, end = next_
if len(ps) == num: answer.append([start+1, end+1, end-start])
if start <= end:
if len(ps) != num and end+1 < len(gems):
start, end = start, end + 1
if gems[end] in ps: ps[gems[end]] += 1
else: ps[gems[end]] = 1
next_ = (start, end)
else:
if gems[start] in ps: ps[gems[start]] -= 1
if ps[gems[start]] == 0: ps.pop(gems[start])
next_ = (start + 1, end)
else: break
answer.sort(key = lambda x :( x[2],x[0]))
return answer[0][0], answer[0][1]문제 4 : [카카오 인턴] 광고 삽입
https://programmers.co.kr/learn/courses/30/lessons/72414
코딩테스트 연습 - 광고 삽입
시간을 나타내는 HH, H1, H2의 범위는 00~99, 분을 나타내는 MM, M1, M2의 범위는 00~59, 초를 나타내는 SS, S1, S2의 범위는 00~59까지 사용됩니다. 잘못된 시각은 입력으로 주어지지 않습니다. (예: 04:60:24, 11
programmers.co.kr
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
문제를 읽고 드는 생각
1. DP로 해결 가능한 문제 인지 지문을 통해 힌트를 얻는다.
모든 시간에 대해 체크하면 완전탐색으로 해결이 가능합니다.
또한 가장 많이 보는 구간을 구해야 합니다.
마지막으로 시각 축에 대해 연속된 구간을 처리하는 문제입니다.
dp를 의심해 봅시다.
2. MEMO시 사용할 DP 테이블의 변수 정하기
카카오의 블라인드 문제는 인턴 문제보다.
구현과 생각해야 할 부분이 많습니다.
인턴 문제에서는 아이디어 1개만 떠올리면 문제해결이 가능한 경우가 많지만,
블라인드의 경우 2개정도의 아이디어가 필요합니다.
이점을 염두해 두고 문제에 대해 생각해 봅시다.
문제를 두 부분으로 나누어 생각해 봅시다.
첫 번째 부분은 0 ~ play_time시간 대에 대하여 각 초마다 몇 명의 사람이 시청했지를 기록하는 정리하는 부분,
두 번째는 정리한 시청기록에서 adv_time이 어디에 위치해야 가장 많은 시청자에게 노출이 되는지로 나누어 생각해 봅시다.
첫 번째 부분의 결과를 저장하는 자료구조는 list를 사용하고 길이가 초로 변환된 play_time의 길이라 생각해 봅시다.
그럼 'dp [초] = 시청자 수'로 생각이 가능합니다.
log기록시 완전탐색으로 log를 돌며 dp에 기록하게 되면 엄청난 시간 복잡도를 소모합니다.
이를 그대로 구현하면 시간초과 판정을 받습니다.
logs를 보면 시작시간과 끝 시간이 있습니다.
이 대이터를 dp테이블에 시작 시간 부터 시작하여 끝시간 까지 +1을 진행해야 합니다.
이를 처리하는 방법으로 아래의 그림처럼 생각해 봅시다.

logs를 dp에 처리하는 방법을 나타낸 그림입니다.
logs를 for loop를 돌며 log를 확인합니다.
dp[log_시작] = 1, dp[log_끝+1] = -1을 기록합니다.
모든 log를 dp에 적용하고 난후에 dp[i] += dp[i-1]점화식을 적용하면 원하는 결과를 볼수 있습니다.
이 알고리즘은 O(len(logs) * play_time) 시간복잡도를 소모합니다.
이는 아래의 코드로 작성한 완전탐색보다 효율적입니다.
for log in logs:
start, end = log
for t in range(start, end):
dp[t] += 1완전탐색의 경우 O( logs[1]*logs[2]*...logs[len(logs)-1])의 시간복잡도를 가집니다.
두번째 부분인 정리한 시청기록에서 adv_time이 어디에 위치해 있는지 찾기위한 방법을 생각해봅시다.

이 그림을 보면 기존에 정리해 두었던 dp에 dp_sum[i] = dp[i] + dp_sum[i-1]점화식으로 dp_sum을 계산하였습니다.
광고의 누적 시청자는 dp_sum[i] - dp_sum[i-ad_time]으로 계산됩니다.
이 알고리즘 방식을 전문용어로 prefix sum 알고리즘이라 합니다.
prefix sum알고리즘은 dp의 기본 유형으로 많이 등장하는 알고리즘이니 한번더 복습해 봅시다.
계산 결과중 가장 크기가 크고 시간대가 앞에 위치한 광고 시간을 리턴하면 됩니다.
위의 그림처럼 dp를 활용한 것이 아니라 완전탐색으로 생각해봅시다.
for s in range(0,len(dp)-ad_time):
n = 0
for t in range(s, s+ad_time):
n += dp[t]
if answer < n: answer = ndp_sum테이블을 사용하지 않은 완전탐색의 경우 O(len(dp)*ad_time)의 시간복잡도가 소모됩니다.
dp_sum을 사용한 경우는 O(len(dp))인 것과 비교하면 엄청 비효율적입니다.
두 번째 부분은 1차원 배열을 탐색하는 부분입니다.
이전에 배웠던 Two pointers알고리즘을 적용할 수 있을까요?
Two pointers알고리즘은 시작 인덱스를 i 끝 인덱스를 j라 했을 때 j-i가 지속적으로 변합니다.
하지만 이번의 경우에는 j-i가 일정합니다.
그래서 안타깝게도 사용하지 못합니다.
하지만 !! 이러한 문제에 대해 효율적으로 탐색하는 방법이 존재합니다.
이 방법을 Sliding Window알고리즘이라 합니다.
간단하게 Sliding Window을 알아봅시다.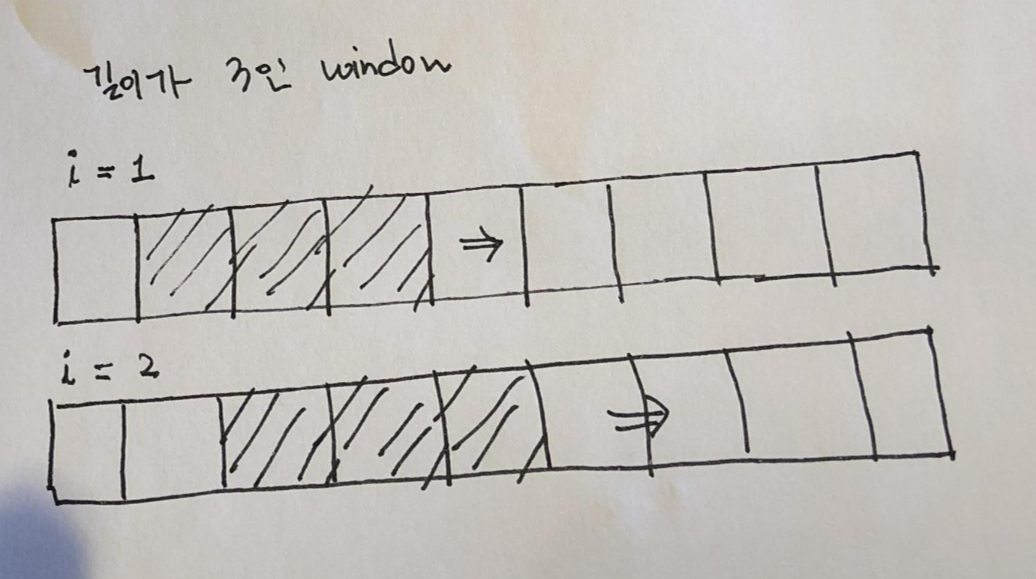
그림은 1차원 배열에 대해 길이가 3인 window가 탐색하는 모습입니다.
이처럼 슬라이딩 윈도우는 길이가 일정한 window를 이용하여 배열을 탐색하는 알고리즘입니다.
슬라이딩 윈도의 경우 아이디어는 간단하지만 구현이 중요합니다.
구현을 봐봅시다.
dp = [0,0,1,2,2,2,2,1,0 ]
window = 3
q = sum(dp[:3])
answer = q
for i in range(1,len(dp)-window):
add_index = i + window - 1
del_index = i - 1
q -= dp[del_index]
q += dp[add_index]
if answer < q: ansewr = q윈도우는 값을 매번 sum(dp[i:j+1])을 이용하여 계산하는 것이 아닌,
q라는 변수를 이용하여 공통으로 관리 함으로써 시간복잡도를 줄이는 알고리즘입니다.
이전 문제에서 공부했던 Two pointers알고리즘 역시 ps = {보석 : 수}자료구조를 공통으로 관리함으로써,
시간복잡도를 상당히 많이 줄일 수 있었습니다.
3. DP의 RECURCE RELATION 찾기
위의 경험을 정리해 봅시다.
#시간대 별로 시청기록을 위한 전처리 : 로그의 시작을 1 끝을 -1로저장
for log in logs:
s, e = log
dp[s] = 1
dp[e+1] = -1
#시청기록 만들기
for i in range(1, len(dp)):
dp[i] += dp[i-1]
#누적 시청기록 만들기
for i in range(1, len(dp)):
dp[i] += dp[i-1]
dp_sum = dp
4. 탐색 방법
광고 시청 최다 구간을 구하기 위해 누적 시청기록(dp_sum)을 이용하여 for loop를 돌며,
dp_sdum[i+ad_time] - dp_sdum[i]를 계산하여 확인하거나
Sliding window 알고리즘 방법으로 시청기록(dp)를 탐색하는 방법이 있습니다.
두가지 모두 구현해 봅시다.
5. 구현 - dp_sum
효
5. 구현 - dp, sliding window
일
'콘텐츠 > 파이썬-알고리즘 기초_ 2021' 카테고리의 다른 글
| 파이썬 - 다이나믹 프로그래밍(dynamic-programming) 문제 풀이 전략 (0) | 2021.12.13 |
|---|---|
| 파이썬 - merge intervals (0) | 2021.12.04 |
| 파이썬 - 이진탐색(binary search) 실전 문제 (0) | 2021.11.24 |
| 파이썬 - graph 실전 문제 (0) | 2021.11.03 |
| 파이썬 - 투 포인터(two pointers) (0) | 2021.11.02 |



